PERCOLATION AND DISORDERED SYSTEMS Geoffrey GRIMMETT

152 Geoffrey Grimmett
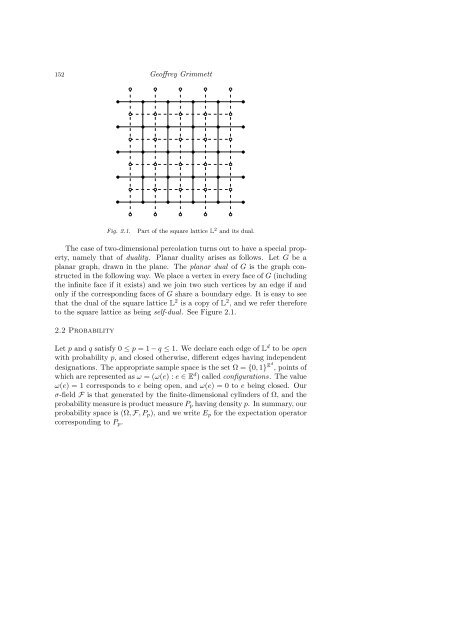
Fig. 2.1. Part of the square lattice L 2 and its dual.
The case of two-dimensional percolation turns out to have a special property,
namely that of duality. Planar duality arises as follows. Let G be a
planar graph, drawn in the plane. The planar dual of G is the graph constructed
in the following way. We place a vertex in every face of G (including
the infinite face if it exists) and we join two such vertices by an edge if and
only if the corresponding faces of G share a boundary edge. It is easy to see
that the dual of the square lattice L 2 is a copy of L 2 , and we refer therefore
to the square lattice as being self-dual. See Figure 2.1.
2.2 Probability
Let p and q satisfy 0 ≤ p = 1 − q ≤ 1. We declare each edge of Ld to be open
with probability p, and closed otherwise, different edges having independent
designations. The appropriate sample space is the set Ω = {0, 1} Ed,
points of
which are represented as ω = (ω(e) : e ∈ Ed ) called configurations. The value
ω(e) = 1 corresponds to e being open, and ω(e) = 0 to e being closed. Our
σ-field F is that generated by the finite-dimensional cylinders of Ω, and the
probability measure is product measure Pp having density p. In summary, our
probability space is (Ω, F, Pp), and we write Ep for the expectation operator
corresponding to Pp.