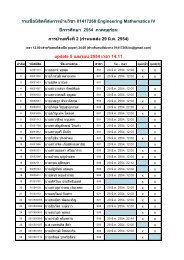
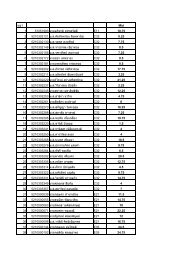
- Page 1 and 2:
A First Course in Complex Analysis
- Page 3:
For Dana, Kasey, and Cody
- Page 6 and 7:
vi Contents Chapter 4. Elementary F
- Page 9 and 10:
Preface 7.2 Preface Philosophy This
- Page 11 and 12:
Preface xi to, but not formally cov
- Page 13 and 14:
3π 2π π 0 -π -2π -3π -1 0 1 -
- Page 15 and 16:
1.1 Complex Numbers and Their Prope
- Page 17 and 18:
1.1 Complex Numbers and Their Prope
- Page 19 and 20:
1.1 Complex Numbers and Their Prope
- Page 21 and 22:
1.1 Complex Numbers and Their Prope
- Page 23 and 24:
y z 2 z 2 - z 1 or (x 2 - x 1 , y 2
- Page 25 and 26:
1.2 Complex Plane 13 From (8) with
- Page 27 and 28:
1.2 Complex Plane 15 30. Find an up
- Page 29 and 30:
O y θ x = r cos θ (r, θ) or (x,
- Page 31 and 32:
1.3 Polar Form of Complex Numbers 1
- Page 33 and 34:
1.3 Polar Form of Complex Numbers 2
- Page 35 and 36:
1.4 Powers and Roots 23 arg(z) =π/
- Page 37 and 38:
√ 4 = 2 and 3 √ 27 = 3 are the
- Page 39 and 40:
1.4 Powers and Roots 27 16. Rework
- Page 41 and 42:
z 0 ρ ρ |z - z 0 |= Figure 1.15 C
- Page 43 and 44:
y Interior Exterior Boundary Figure
- Page 45 and 46:
1.5 Sets of Points in the Complex P
- Page 47 and 48:
1.5 Sets of Points in the Complex P
- Page 49 and 50:
Note: The roots z1 and z2 are conju
- Page 51 and 52:
1.6 Applications 39 c = 0.The latte
- Page 53 and 54:
1.6 Applications 41 Electrical engi
- Page 55 and 56:
1.6 Applications 43 In Problems 25
- Page 57 and 58:
Chapter 1 Review Quiz 45 Here the s
- Page 59 and 60:
Chapter 1 Review Quiz 47 27. The pr
- Page 61 and 62:
3i 2i i S 1 2 3 Image of a square u
- Page 63 and 64:
2.1 Complex Functions 51 interchang
- Page 65 and 66:
2.1 Complex Functions 53 Definition
- Page 67 and 68:
2.1 Complex Functions 55 respective
- Page 69 and 70:
2.1 Complex Functions 57 Focus on C
- Page 71 and 72:
2.2 Complex Functions as Mappings 5
- Page 73 and 74:
-4 -4 -3 C 2 3 4 (a) The vertical l
- Page 75 and 76:
2.2 Complex Functions as Mappings 6
- Page 77 and 78:
4 2 -6 -4 -2 2 4 6 -2 -4 v Figure 2
- Page 79 and 80:
2.2 Complex Functions as Mappings 6
- Page 81 and 82:
3i 2i i S z 1 2 3 S′ T(z) Figure
- Page 83 and 84:
ar Figure 2.12 Magnification C C′
- Page 85 and 86:
Note: The order in which you perfor
- Page 87 and 88:
2.3 Linear Mappings 75 triangle S4
- Page 89 and 90:
2.3 Linear Mappings 77 In Problems
- Page 91 and 92:
2.3 Linear Mappings 79 36. (a) Give
- Page 93 and 94:
2θ r θ r 2 Figure 2.17 The mappin
- Page 95 and 96:
-3 y 3 2 1 -2 -1 1 2 3 -1 -2 -3 (a)
- Page 97 and 98:
y 2 1.5 1 0.5 -2 -1.5 -1 -0.5 -0.5
- Page 99 and 100:
Note ☞ 2.4 Special Power Function
- Page 101 and 102:
Solve the equation z = f(w) for w t
- Page 103 and 104:
Remember: Arg(z) is in the interval
- Page 105 and 106:
S y (a) A circular sector 3π/8 v 3
- Page 107 and 108:
B y y A w = z 2 x (a) A maps onto A
- Page 109 and 110:
3π 2π π 0 -π -2π -3π -1 0 1 -
- Page 111 and 112:
2.4 Special Power Functions 99 43.
- Page 113 and 114:
z c(z) Figure 2.41 Complex conjugat
- Page 115 and 116:
w = 1/z Figure 2.43 The reciprocal
- Page 117 and 118:
2.5 Reciprocal Function 105 of the
- Page 119 and 120:
2.5 Reciprocal Function 107 underst
- Page 121 and 122:
2.5 Reciprocal Function 109 24. Acc
- Page 123 and 124:
L y y = L + ε y = L - ε y = f(x)
- Page 125 and 126:
2.6 Limits and Continuity 113 Crite
- Page 127 and 128:
2.6 Limits and Continuity 115 Befor
- Page 129 and 130: 2.6 Limits and Continuity 117 Theor
- Page 131 and 132: 2.6 Limits and Continuity 119 See (
- Page 133 and 134: -1 y z = e iθ Figure 2.54 Figure f
- Page 135 and 136: 2.6 Limits and Continuity 123 It th
- Page 137 and 138: 2.6 Limits and Continuity 125 While
- Page 139 and 140: y Values of arg decreasing Values o
- Page 141 and 142: 2.6 Limits and Continuity 129 In Pr
- Page 143 and 144: 2.6 Limits and Continuity 131 In Pr
- Page 145 and 146: -4 -4 -3 -2 (-2, -1) 4 3 2 1 y -1 1
- Page 147 and 148: Note: Normalized vector fields shou
- Page 149 and 150: 4 2 y -4 -2 2 4 -2 -4 Figure 2.63 S
- Page 151 and 152: Chapter 2 Review Quiz 139 10. The l
- Page 153 and 154: 3 2 1 0 -1 -2 -3 -3 -2 -1 0 1 2 3 L
- Page 155 and 156: 3.1 Differentiability and Analytici
- Page 157 and 158: ☞ 3.1 Differentiability and Analy
- Page 159 and 160: 3.1 Differentiability and Analytici
- Page 161 and 162: 3.1 Differentiability and Analytici
- Page 163 and 164: 3.1 Differentiability and Analytici
- Page 165 and 166: 3.2 Cauchy-Riemann Equations 153 We
- Page 167 and 168: 3.2 Cauchy-Riemann Equations 155 EX
- Page 169 and 170: 3.2 Cauchy-Riemann Equations 157 EX
- Page 171 and 172: 3.3 Harmonic Functions 159 then sol
- Page 173 and 174: 3.3 Harmonic Functions 161 EXAMPLE
- Page 175 and 176: 3.3 Harmonic Functions 163 In Probl
- Page 177 and 178: 3.4 Applications 165 tangent is the
- Page 179: Lines of force ψ = c2 Lower potent
- Page 183 and 184: y a b φ = k 1 x φ = k 0 Figure 3.
- Page 185: Chapter 3 Review Quiz 173 11. The C
- Page 188 and 189: 176 Chapter 4 Elementary Functions
- Page 190 and 191: 178 Chapter 4 Elementary Functions
- Page 192 and 193: 180 Chapter 4 Elementary Functions
- Page 194 and 195: 182 Chapter 4 Elementary Functions
- Page 196 and 197: 184 Chapter 4 Elementary Functions
- Page 198 and 199: 186 Chapter 4 Elementary Functions
- Page 200 and 201: 188 Chapter 4 Elementary Functions
- Page 202 and 203: 190 Chapter 4 Elementary Functions
- Page 204 and 205: 192 Chapter 4 Elementary Functions
- Page 206 and 207: 194 Chapter 4 Elementary Functions
- Page 208 and 209: 196 Chapter 4 Elementary Functions
- Page 210 and 211: 198 Chapter 4 Elementary Functions
- Page 212 and 213: 200 Chapter 4 Elementary Functions
- Page 214 and 215: 202 Chapter 4 Elementary Functions
- Page 216 and 217: 204 Chapter 4 Elementary Functions
- Page 218 and 219: 206 Chapter 4 Elementary Functions
- Page 220 and 221: 208 Chapter 4 Elementary Functions
- Page 222 and 223: 210 Chapter 4 Elementary Functions
- Page 224 and 225: 212 Chapter 4 Elementary Functions
- Page 226 and 227: 214 Chapter 4 Elementary Functions
- Page 228 and 229: 216 Chapter 4 Elementary Functions
- Page 230 and 231:
218 Chapter 4 Elementary Functions
- Page 232 and 233:
220 Chapter 4 Elementary Functions
- Page 234 and 235:
222 Chapter 4 Elementary Functions
- Page 236 and 237:
224 Chapter 4 Elementary Functions
- Page 238 and 239:
226 Chapter 4 Elementary Functions
- Page 240 and 241:
228 Chapter 4 Elementary Functions
- Page 242 and 243:
230 Chapter 4 Elementary Functions
- Page 244 and 245:
232 Chapter 4 Elementary Functions
- Page 247 and 248:
Normalized velocity vector field fo
- Page 249 and 250:
5.1 Real Integrals 237 3. Let �P
- Page 251 and 252:
y π t = gives 2 (0,4) C t = 0 give
- Page 253 and 254:
(-1, -1) y C (2, 8) x Figure 5.5 Gr
- Page 255 and 256:
5.1 Real Integrals 243 denotes the
- Page 257 and 258:
5.2 Complex Integrals 245 In Proble
- Page 259 and 260:
z 0 C z k * z 1 * z 2 * z 2 z 1 z k
- Page 261 and 262:
These properties are important in t
- Page 263 and 264:
5.2 Complex Integrals 251 Now in vi
- Page 265 and 266:
5.2 Complex Integrals 253 Proof It
- Page 267 and 268:
y 1 + i 1 Figure 5.21 Figure for Pr
- Page 269 and 270:
D C Figure 5.26 Simply connected do
- Page 271 and 272:
D D A C C (a) (b) B C 1 C 1 Figure
- Page 273 and 274:
C 1 C 1 C (a) C (b) Figure 5.31 Tri
- Page 275 and 276:
C C y Figure 5.34 Figure for Proble
- Page 277 and 278:
z 0 C 1 D z 1 C Figure 5.38 If f is
- Page 279 and 280:
5.4 Independence of Path 267 and z(
- Page 281 and 282:
Be careful when using Ln z as an an
- Page 283 and 284:
5.4 Independence of Path 271 (ii) I
- Page 285 and 286:
5.5 Cauchy’s Integral Formulas an
- Page 287 and 288:
3i -3i y Figure 5.44 Contour for Ex
- Page 289 and 290:
y i 0 C 2 C 1 Figure 5.45 Contour f
- Page 291 and 292:
5.5 Cauchy’s Integral Formulas an
- Page 293 and 294:
5.5 Cauchy’s Integral Formulas an
- Page 295 and 296:
5.5 Cauchy’s Integral Formulas an
- Page 297 and 298:
5.6 Applications 285 A B A B A B (a
- Page 299 and 300:
5.6 Applications 287 Indeed, by rew
- Page 301 and 302:
Note ☞ 5.6 Applications 289 If yo
- Page 303 and 304:
-2 -1 2 1 -1 -2 y Figure 5.51 Zero
- Page 305 and 306:
-1 -0.5 1 0.5 -0.5 -1 y 0.5 Figure
- Page 307 and 308:
5.6 Applications 295 In Problems 5-
- Page 309 and 310:
C 1 y 2i C 2 -2 2 Figure 5.58 Figur
- Page 311:
Chapter 5 Review Quiz 299 � z 38.
- Page 314 and 315:
302 Chapter 6 Series and Residues y
- Page 316 and 317:
304 Chapter 6 Series and Residues Y
- Page 318 and 319:
306 Chapter 6 Series and Residues D
- Page 320 and 321:
308 Chapter 6 Series and Residues E
- Page 322 and 323:
310 Chapter 6 Series and Residues R
- Page 324 and 325:
312 Chapter 6 Series and Residues 3
- Page 326 and 327:
314 Chapter 6 Series and Residues I
- Page 328 and 329:
316 Chapter 6 Series and Residues D
- Page 330 and 331:
318 Chapter 6 Series and Residues N
- Page 332 and 333:
320 Chapter 6 Series and Residues y
- Page 334 and 335:
322 Chapter 6 Series and Residues 2
- Page 336 and 337:
324 Chapter 6 Series and Residues I
- Page 338 and 339:
326 Chapter 6 Series and Residues a
- Page 340 and 341:
328 Chapter 6 Series and Residues N
- Page 342 and 343:
330 Chapter 6 Series and Residues T
- Page 344 and 345:
332 Chapter 6 Series and Residues y
- Page 346 and 347:
334 Chapter 6 Series and Residues R
- Page 348 and 349:
336 Chapter 6 Series and Residues i
- Page 350 and 351:
338 Chapter 6 Series and Residues A
- Page 352 and 353:
340 Chapter 6 Series and Residues S
- Page 354 and 355:
342 Chapter 6 Series and Residues 3
- Page 356 and 357:
344 Chapter 6 Series and Residues T
- Page 358 and 359:
346 Chapter 6 Series and Residues (
- Page 360 and 361:
348 Chapter 6 Series and Residues E
- Page 362 and 363:
350 Chapter 6 Series and Residues 4
- Page 364 and 365:
352 Chapter 6 Series and Residues (
- Page 366 and 367:
354 Chapter 6 Series and Residues H
- Page 368 and 369:
356 Chapter 6 Series and Residues -
- Page 370 and 371:
358 Chapter 6 Series and Residues o
- Page 372 and 373:
360 Chapter 6 Series and Residues -
- Page 374 and 375:
362 Chapter 6 Series and Residues z
- Page 376 and 377:
364 Chapter 6 Series and Residues f
- Page 378 and 379:
366 Chapter 6 Series and Residues v
- Page 380 and 381:
368 Chapter 6 Series and Residues
- Page 382 and 383:
370 Chapter 6 Series and Residues E
- Page 384 and 385:
372 Chapter 6 Series and Residues 5
- Page 386 and 387:
374 Chapter 6 Series and Residues I
- Page 388 and 389:
376 Chapter 6 Series and Residues y
- Page 390 and 391:
378 Chapter 6 Series and Residues C
- Page 392 and 393:
380 Chapter 6 Series and Residues s
- Page 394 and 395:
382 Chapter 6 Series and Residues 1
- Page 396 and 397:
384 Chapter 6 Series and Residues (
- Page 398 and 399:
386 Chapter 6 Series and Residues P
- Page 400 and 401:
388 Chapter 6 Series and Residues 3
- Page 402 and 403:
390 Chapter 7 Conformal Mappings y
- Page 404 and 405:
392 Chapter 7 Conformal Mappings y
- Page 406 and 407:
394 Chapter 7 Conformal Mappings π
- Page 408 and 409:
396 Chapter 7 Conformal Mappings Re
- Page 410 and 411:
398 Chapter 7 Conformal Mappings 15
- Page 412 and 413:
400 Chapter 7 Conformal Mappings De
- Page 414 and 415:
402 Chapter 7 Conformal Mappings Th
- Page 416 and 417:
404 Chapter 7 Conformal Mappings v
- Page 418 and 419:
406 Chapter 7 Conformal Mappings Re
- Page 420 and 421:
408 Chapter 7 Conformal Mappings No
- Page 422 and 423:
410 Chapter 7 Conformal Mappings y
- Page 424 and 425:
412 Chapter 7 Conformal Mappings x
- Page 426 and 427:
414 Chapter 7 Conformal Mappings A
- Page 428 and 429:
416 Chapter 7 Conformal Mappings fo
- Page 430 and 431:
418 Chapter 7 Conformal Mappings EX
- Page 432 and 433:
420 Chapter 7 Conformal Mappings
- Page 434 and 435:
422 Chapter 7 Conformal Mappings y
- Page 436 and 437:
424 Chapter 7 Conformal Mappings y
- Page 438 and 439:
426 Chapter 7 Conformal Mappings y
- Page 440 and 441:
428 Chapter 7 Conformal Mappings (a
- Page 442 and 443:
430 Chapter 7 Conformal Mappings y
- Page 444 and 445:
432 Chapter 7 Conformal Mappings 3
- Page 446 and 447:
434 Chapter 7 Conformal Mappings y
- Page 448 and 449:
436 Chapter 7 Conformal Mappings φ
- Page 450 and 451:
438 Chapter 7 Conformal Mappings ψ
- Page 452 and 453:
440 Chapter 7 Conformal Mappings y
- Page 454 and 455:
442 Chapter 7 Conformal Mappings 4
- Page 456 and 457:
444 Chapter 7 Conformal Mappings In
- Page 458 and 459:
446 Chapter 7 Conformal Mappings 24
- Page 460 and 461:
448 Chapter 7 Conformal Mappings In
- Page 463 and 464:
Appendixes 1
- Page 465 and 466:
Appendix II Proof of the Cauchy-Gou
- Page 467 and 468:
Integrals � � � FE , GF , EG
- Page 469 and 470:
Appendix I Proof of Theorem 2.1 APP
- Page 471 and 472:
Appendix III Table of Conformal Map
- Page 473 and 474:
Appendix III Table of Conformal Map
- Page 475 and 476:
Appendix III Table of Conformal Map
- Page 477 and 478:
Appendix III Table of Conformal Map
- Page 479 and 480:
Answers to Selected Odd-Numbered Pr
- Page 481 and 482:
Answers to Selected Odd-Numbered Pr
- Page 483 and 484:
Answers to Selected Odd-Numbered Pr
- Page 485 and 486:
Answers to Selected Odd-Numbered Pr
- Page 487 and 488:
Answers to Selected Odd-Numbered Pr
- Page 489 and 490:
Answers to Selected Odd-Numbered Pr
- Page 491 and 492:
Answers to Selected Odd-Numbered Pr
- Page 493 and 494:
Answers to Selected Odd-Numbered Pr
- Page 495 and 496:
Answers to Selected Odd-Numbered Pr
- Page 497 and 498:
Answers to Selected Odd-Numbered Pr
- Page 499 and 500:
Answers to Selected Odd-Numbered Pr
- Page 501 and 502:
Answers to Selected Odd-Numbered Pr
- Page 503 and 504:
Indexes 1
- Page 505 and 506:
Word Index IND-7 Convergence of an
- Page 507 and 508:
Word Index IND-5 Cauchy-Riemann equ
- Page 509 and 510:
Symbol Index IND-3 z α , 194 sin z
- Page 511 and 512:
Word Index IND-9 principal square r
- Page 513 and 514:
IND-14 Word Index partial sums of,
- Page 515 and 516:
IND-12 Word Index Partial fractions
- Page 517:
Word Index IND-15 mapping by, 206-2