¨Ubungsblatt 1
¨Ubungsblatt 1
¨Ubungsblatt 1
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
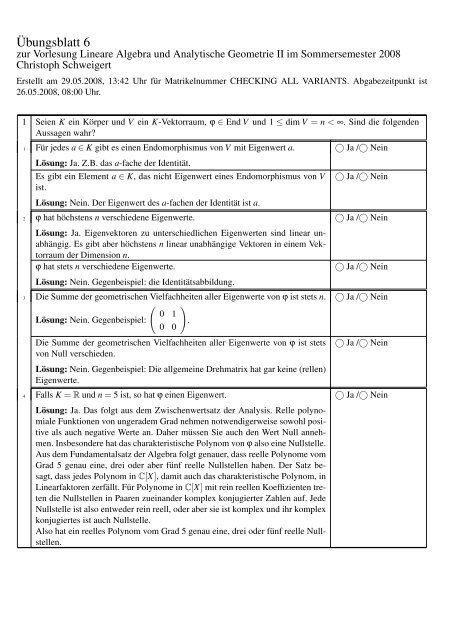
Übungsblatt 6<br />
zur Vorlesung Lineare Algebra und Analytische Geometrie II im Sommersemester 2008<br />
Christoph Schweigert<br />
Erstellt am 29.05.2008, 13:42 Uhr für Matrikelnummer CHECKING ALL VARIANTS. Abgabezeitpunkt ist<br />
26.05.2008, 08:00 Uhr.<br />
1 Seien K ein Körper und V ein K-Vektorraum, ϕ ∈ End V und 1 ≤ dim V = n < ∞. Sind die folgenden<br />
Aussagen wahr?<br />
1 Für jedes a ∈ K gibt es einen Endomorphismus von V mit Eigenwert a.<br />
Lösung: Ja. Z.B. das a-fache der Identität.<br />
Es gibt ein Element a ∈ K, das nicht Eigenwert eines Endomorphismus von V<br />
ist.<br />
Lösung: Nein. Der Eigenwert des a-fachen der Identität ist a.<br />
2 ϕ hat höchstens n verschiedene Eigenwerte.<br />
Lösung: Ja. Eigenvektoren zu unterschiedlichen Eigenwerten sind linear unabhängig.<br />
Es gibt aber höchstens n linear unabhängige Vektoren in einem Vektorraum<br />
der Dimension n.<br />
ϕ hat stets n verschiedene Eigenwerte.<br />
Lösung: Nein. Gegenbeispiel: die Identitätsabbildung.<br />
3 Die Summe der geometrischen Vielfachheiten aller Eigenwerte von ϕ ist stets n.<br />
( )<br />
0 1<br />
Lösung: Nein. Gegenbeispiel: .<br />
0 0<br />
Die Summe der geometrischen Vielfachheiten aller Eigenwerte von ϕ ist stets<br />
von Null verschieden.<br />
Lösung: Nein. Gegenbeispiel: Die allgemeine Drehmatrix hat gar keine (rellen)<br />
Eigenwerte.<br />
4 Falls K = R und n = 5 ist, so hat ϕ einen Eigenwert.<br />
Lösung: Ja. Das folgt aus dem Zwischenwertsatz der Analysis. Relle polynomiale<br />
Funktionen von ungeradem Grad nehmen notwendigerweise sowohl positive<br />
als auch negative Werte an. Daher müssen Sie auch den Wert Null annehmen.<br />
Insbesondere hat das charakteristische Polynom von ϕ also eine Nullstelle.<br />
Aus dem Fundamentalsatz der Algebra folgt genauer, dass reelle Polynome vom<br />
Grad 5 genau eine, drei oder aber fünf reelle Nullstellen haben. Der Satz besagt,<br />
dass jedes Polynom in C[X], damit auch das charakteristische Polynom, in<br />
Linearfaktoren zerfällt. Für Polynome in C[X] mit rein reellen Koeffizienten treten<br />
die Nullstellen in Paaren zueinander komplex konjugierter Zahlen auf. Jede<br />
Nullstelle ist also entweder rein reell, oder aber sie ist komplex und ihr komplex<br />
konjugiertes ist auch Nullstelle.<br />
Also hat ein reelles Polynom vom Grad 5 genau eine, drei oder fünf reelle Nullstellen.<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein