¨Ubungsblatt 1

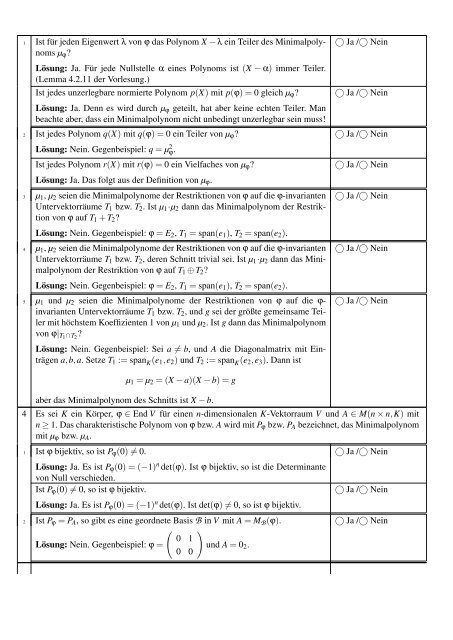
1 Ist für jeden Eigenwert λ von ϕ das Polynom X − λ ein Teiler des Minimalpolynoms
µ ϕ ?
Lösung: Ja. Für jede Nullstelle α eines Polynoms ist (X − α) immer Teiler.
(Lemma 4.2.11 der Vorlesung.)
Ist jedes unzerlegbare normierte Polynom p(X) mit p(ϕ) = 0 gleich µ ϕ ?
Lösung: Ja. Denn es wird durch µ ϕ geteilt, hat aber keine echten Teiler. Man
beachte aber, dass ein Minimalpolynom nicht unbedingt unzerlegbar sein muss!
2 Ist jedes Polynom q(X) mit q(ϕ) = 0 ein Teiler von µ ϕ ?
Lösung: Nein. Gegenbeispiel: q = µ 2 ϕ.
Ist jedes Polynom r(X) mit r(ϕ) = 0 ein Vielfaches von µ ϕ ?
Lösung: Ja. Das folgt aus der Definition von µ ϕ .
3 µ 1 , µ 2 seien die Minimalpolynome der Restriktionen von ϕ auf die ϕ-invarianten
Untervektorräume T 1 bzw. T 2 . Ist µ 1·µ 2 dann das Minimalpolynom der Restriktion
von ϕ auf T 1 + T 2 ?
Lösung: Nein. Gegenbeispiel: ϕ = E 2 , T 1 = span(e 1 ), T 2 = span(e 2 ).
4 µ 1 , µ 2 seien die Minimalpolynome der Restriktionen von ϕ auf die ϕ-invarianten
Untervektorräume T 1 bzw. T 2 , deren Schnitt trivial sei. Ist µ 1·µ 2 dann das Minimalpolynom
der Restriktion von ϕ auf T 1 ⊕ T 2 ?
Lösung: Nein. Gegenbeispiel: ϕ = E 2 , T 1 = span(e 1 ), T 2 = span(e 2 ).
5 µ 1 und µ 2 seien die Minimalpolynome der Restriktionen von ϕ auf die ϕ-
invarianten Untervektorräume T 1 bzw. T 2 , und g sei der größte gemeinsame Teiler
mit höchstem Koeffizienten 1 von µ 1 und µ 2 . Ist g dann das Minimalpolynom
von ϕ| T1 ∩T 2
?
Lösung: Nein. Gegenbeispiel: Sei a ≠ b, und A die Diagonalmatrix mit Einträgen
a,b,a. Setze T 1 := span K (e 1 ,e 2 ) und T 2 := span K (e 2 ,e 3 ). Dann ist
○ Ja /○ Nein
○ Ja /○ Nein
○ Ja /○ Nein
○ Ja /○ Nein
○ Ja /○ Nein
○ Ja /○ Nein
○ Ja /○ Nein
µ 1 = µ 2 = (X − a)(X − b) = g
aber das Minimalpolynom des Schnitts ist X − b.
4 Es sei K ein Körper, ϕ ∈ End V für einen n-dimensionalen K-Vektorraum V und A ∈ M(n × n,K) mit
n ≥ 1. Das charakteristische Polynom von ϕ bzw. A wird mit P ϕ bzw. P A bezeichnet, das Minimalpolynom
mit µ ϕ bzw. µ A .
1 Ist ϕ bijektiv, so ist P ϕ (0) ≠ 0.
Lösung: Ja. Es ist P ϕ (0) = (−1) n det(ϕ). Ist ϕ bijektiv, so ist die Determinante
von Null verschieden.
Ist P ϕ (0) ≠ 0, so ist ϕ bijektiv.
Lösung: Ja. Es ist P ϕ (0) = (−1) n det(ϕ). Ist det(ϕ) ≠ 0, so ist ϕ bijektiv.
2 Ist P ϕ = P A , so gibt es eine geordnete Basis B in V mit A = M B (ϕ).
( )
0 1
Lösung: Nein. Gegenbeispiel: ϕ = und A = 0 2 .
0 0
○ Ja /○ Nein
○ Ja /○ Nein
○ Ja /○ Nein