¨Ubungsblatt 1
¨Ubungsblatt 1
¨Ubungsblatt 1
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
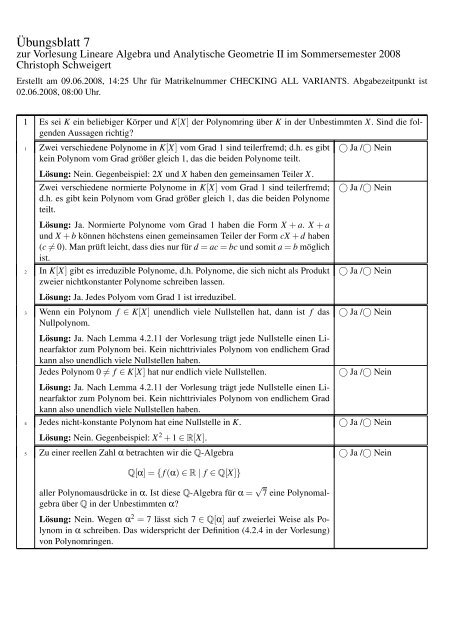
Übungsblatt 7<br />
zur Vorlesung Lineare Algebra und Analytische Geometrie II im Sommersemester 2008<br />
Christoph Schweigert<br />
Erstellt am 09.06.2008, 14:25 Uhr für Matrikelnummer CHECKING ALL VARIANTS. Abgabezeitpunkt ist<br />
02.06.2008, 08:00 Uhr.<br />
1 Es sei K ein beliebiger Körper und K[X] der Polynomring über K in der Unbestimmten X. Sind die folgenden<br />
Aussagen richtig?<br />
1 Zwei verschiedene Polynome in K[X] vom Grad 1 sind teilerfremd; d.h. es gibt<br />
kein Polynom vom Grad größer gleich 1, das die beiden Polynome teilt.<br />
Lösung: Nein. Gegenbeispiel: 2X und X haben den gemeinsamen Teiler X.<br />
Zwei verschiedene normierte Polynome in K[X] vom Grad 1 sind teilerfremd;<br />
d.h. es gibt kein Polynom vom Grad größer gleich 1, das die beiden Polynome<br />
teilt.<br />
Lösung: Ja. Normierte Polynome vom Grad 1 haben die Form X + a. X + a<br />
und X + b können höchstens einen gemeinsamen Teiler der Form cX + d haben<br />
(c ≠ 0). Man prüft leicht, dass dies nur für d = ac = bc und somit a = b möglich<br />
ist.<br />
2 In K[X] gibt es irreduzible Polynome, d.h. Polynome, die sich nicht als Produkt<br />
zweier nichtkonstanter Polynome schreiben lassen.<br />
Lösung: Ja. Jedes Polyom vom Grad 1 ist irreduzibel.<br />
3 Wenn ein Polynom f ∈ K[X] unendlich viele Nullstellen hat, dann ist f das<br />
Nullpolynom.<br />
Lösung: Ja. Nach Lemma 4.2.11 der Vorlesung trägt jede Nullstelle einen Linearfaktor<br />
zum Polynom bei. Kein nichttriviales Polynom von endlichem Grad<br />
kann also unendlich viele Nullstellen haben.<br />
Jedes Polynom 0 ≠ f ∈ K[X] hat nur endlich viele Nullstellen.<br />
Lösung: Ja. Nach Lemma 4.2.11 der Vorlesung trägt jede Nullstelle einen Linearfaktor<br />
zum Polynom bei. Kein nichttriviales Polynom von endlichem Grad<br />
kann also unendlich viele Nullstellen haben.<br />
4 Jedes nicht-konstante Polynom hat eine Nullstelle in K.<br />
Lösung: Nein. Gegenbeispiel: X 2 + 1 ∈ R[X].<br />
5 Zu einer reellen Zahl α betrachten wir die Q-Algebra<br />
Q[α] = { f (α) ∈ R | f ∈ Q[X]}<br />
aller Polynomausdrücke in α. Ist diese Q-Algebra für α = √ 7 eine Polynomalgebra<br />
über Q in der Unbestimmten α?<br />
Lösung: Nein. Wegen α 2 = 7 lässt sich 7 ∈ Q[α] auf zweierlei Weise als Polynom<br />
in α schreiben. Das widerspricht der Definition (4.2.4 in der Vorlesung)<br />
von Polynomringen.<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein<br />
○ Ja /○ Nein