The role of metacognitive skills in learning to solve problems

More documents

Recommendations

Info

$Learning LATEX by Doing$

130 model condition. Perhaps, performing the activities of the KM model enables active use of concepts and the relations between them in the domain of KM, which explains why the correlation is stronger in the model condition than in the no-model condition. The data do not support the existence of a relation between the selfreported use of metacognitive skills and learning success. Neither selfreport measures of metacognition are related to any post-test measures of learning. Also, when controlling for pre-test measures, no significant correlation coefficients are found. If a significant correlation exists between learning success and the concurrent measure of metacognition, then hypothesis 5 can be accepted. This is investigated in section 6.3.3.3. Hypothesis 6 concerns a significant relation between post-test measures of learning and transfer. This hypothesis is supported by the results, since all post-test measures of learning are strongly related to results on the transfer test. KM Quest apparently triggers transfer of knowledge. This effect is stronger in the model condition than in the nomodel condition. No differences exist however between both conditions. Perhaps the KM model in KM Quest facilitates transfer of knowledge to another setting even more. In the model condition, the relation between declarative knowledge and transfer is very strong (r = 0.71). This might again be explained by the fact that students in the model condition actively have to use declarative knowledge in order to perform activities in the KM model. This would cause the application of this knowledge to an alternative case to be more easy. Finally, concerning hypothesis 7, the relation between measurements of metacognition and transfer of knowledge, the self-report measures do not show any significant relation with transfer. No relation exists between the use of metacognitive skills and the ability to transfer knowledge to another case. Hypothesis 7 could not be confirmed with regard to self-report measures of metacognition. Concerning the relation between game results and post-test measures of learning (measured at team-level), no significant correlation coefficient could be reported. How well teams have played the game is therefore not an indication that knowledge acquisition actually takes place. 6.3.3 Concurrent measurement 6.3.3.1 Differences between conditions in concurrent measures Protocol analysis was performed manually on over 17,000 chat contributions of team members. The contributions covered all communication
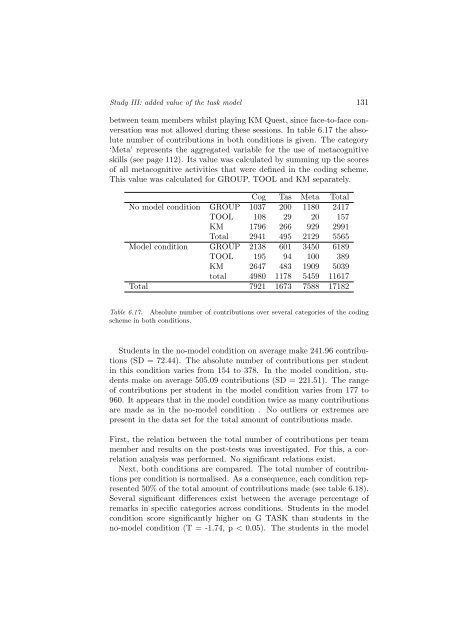
Study III: added value of the task model 131 between team members whilst playing KM Quest, since face-to-face conversation was not allowed during these sessions. In table 6.17 the absolute number of contributions in both conditions is given. The category ‘Meta’ represents the aggregated variable for the use of metacognitive skills (see page 112). Its value was calculated by summing up the scores of all metacognitive activities that were defined in the coding scheme. This value was calculated for GROUP, TOOL and KM separately. Cog Tas Meta Total No model condition GROUP 1037 200 1180 2417 TOOL 108 29 20 157 KM 1796 266 929 2991 Total 2941 495 2129 5565 Model condition GROUP 2138 601 3450 6189 TOOL 195 94 100 389 KM 2647 483 1909 5039 total 4980 1178 5459 11617 Total 7921 1673 7588 17182 Table 6.17. Absolute number of contributions over several categories of the coding scheme in both conditions. Students in the no-model condition on average make 241.96 contributions (SD = 72.44). The absolute number of contributions per student in this condition varies from 154 to 378. In the model condition, students make on average 505.09 contributions (SD = 221.51). The range of contributions per student in the model condition varies from 177 to 960. It appears that in the model condition twice as many contributions are made as in the no-model condition . No outliers or extremes are present in the data set for the total amount of contributions made. First, the relation between the total number of contributions per team member and results on the post-tests was investigated. For this, a correlation analysis was performed. No significant relations exist. Next, both conditions are compared. The total number of contributions per condition is normalised. As a consequence, each condition represented 50% of the total amount of contributions made (see table 6.18). Several significant differences exist between the average percentage of remarks in specific categories across conditions. Students in the model condition score significantly higher on G TASK than students in the no-model condition (T = -1.74, p < 0.05). The students in the model
Page 1 and 2:
The role of metacognitive skills in
Page 3 and 4:
The role of metacognitive skills in
Page 5 and 6:
Contents 1. INTRODUCTION 1 2. THEOR
Page 7:
Contents ix 6. STUDY III: ADDED VAL
Page 10 and 11:
xii Rienke Schutte, zonder de medew
Page 12 and 13:
2 in realistic settings and everyda
Page 14 and 15:
4 use a trade-off between efforts i
Page 16 and 17:
6 of this thesis are described. In
Page 18 and 19:
8 First an overview of relevant lit
Page 20 and 21:
10 In research concerning reading a
Page 22 and 23:
12 problem has actually been found
Page 24 and 25:
14 or whether domain specific metac
Page 26 and 27:
16 learners should be able to artic
Page 28 and 29:
18 piece of origami paper. Both mat
Page 30 and 31:
20 tion given to the problem solver
Page 32 and 33:
22 is rather directive. It does not
Page 34 and 35:
24 The problem solver has declarati
Page 36 and 37:
26 problem and the fact that studen
Page 38 and 39:
28 learn from them. In terms of Jan
Page 40 and 41:
30 This model is called DORMOBILE (
Page 42 and 43:
32 Second, the meta-level in proble
Page 44 and 45:
34 Figure 2.8. Theoretical model of
Page 46 and 47:
36 task-level. In order to keep the
Page 49 and 50:
Chapter 3 KM QUEST The goal of this
Page 51 and 52:
KM Quest 41 Figure 3.1. The Knowled
Page 53 and 54:
KM Quest 43 the fact that some plan
Page 55 and 56:
KM Quest 45 a dynamic simulation-ga
Page 57 and 58:
KM Quest 47 Quest. They are visuali
Page 59 and 60:
KM Quest 49 cesses in Coltec. For e
Page 61 and 62:
KM Quest 51 Figure 3.5. The Knowled
Page 63 and 64:
KM Quest 53 3.3.1.3 The IMPLEMENT p
Page 65 and 66:
KM Quest 55 process in an electroni
Page 67 and 68:
Chapter 4 STUDY I: PILOT This chapt
Page 69 and 70:
Study I: Pilot 59 the spontaneous o
Page 71 and 72:
Study I: Pilot 61 Also, the questio
Page 73 and 74:
Study I: Pilot 63 however, to what
Page 75 and 76:
Study I: Pilot 65 ceived 12 questio
Page 77 and 78:
Study I: Pilot 67 objective, a seco
Page 79 and 80:
Study I: Pilot 69 other. It also ex
Page 81 and 82:
Study I: Pilot 71 In conclusion, th
Page 83 and 84:
Study I: Pilot 73 Finally, the othe
Page 85 and 86:
Study I: Pilot 75 Figure 4.2. Scree
Page 87 and 88:
Study I: Pilot 77 Figure 4.4. Scree
Page 89 and 90: Study I: Pilot 79 Figure 4.5. Scree
Page 91 and 92: Study I: Pilot 81 Figure 4.7. Scree
Page 93: Study I: Pilot 83 alizations of the
Page 96 and 97: 86 of meaningful learning which can
Page 98 and 99: 88 opportunity events (instead of t
Page 100 and 101: 90 different occasions or settings.
Page 102 and 103: 92 conceptual correctness (54) the
Page 104 and 105: 94 The score on KMQUESTions indicat
Page 106 and 107: 96 is a variable that influences th
Page 108 and 109: 98 5.4 Discussion The hypothesis fo
Page 110 and 111: 100 mal company results. In the fol
Page 112 and 113: 102 more inclined to regulate domai
Page 114 and 115: 104 these skills in order to solve
Page 116 and 117: 106 Hypothesis 1: students acquire
Page 118 and 119: 108 KMQUESTions of study II was per
Page 120 and 121: 110 The second measurement of game
Page 122 and 123: 112 T-PROS because they did not occ
Page 124 and 125: 114 Category Rule Example Task Indi
Page 126 and 127: 116 vised by one experimenter in or
Page 128 and 129: 118 6.3 Results 6.3.1 Game results
Page 130 and 131: 120 to Coltec. Only threats have a
Page 132 and 133: 122 6.3.2.1 Effects of learning and
Page 134 and 135: 124 Prospective Pre-test Post-test
Page 136 and 137: 126 Distribution Frequency 1 high 2
Page 138 and 139: 128 No − model Model Retrospectiv
Page 142 and 143: 132 Cog Tas Meta Total No-model con
Page 144 and 145: 134 Condition * Metacognition G MET
Page 146 and 147: 136 Figure 6.5. Relations between m
Page 148 and 149: 138 in the model condition: Visuali
Page 150 and 151: 140 Figure 6.7. Overview of relatio
Page 152 and 153: 142 ‘monitoring’. Prospective s
Page 154 and 155: 144 learning. Finally, in the no-mo
Page 156 and 157: 146 inclusion of a task model speci
Page 158 and 159: 148 interpreting the results on met
Page 160 and 161: 150 When no task model is available
Page 162 and 163: 152 Another perhaps more valid expl
Page 164 and 165: 154 havioural measures prove to be
Page 167 and 168: Appendix A Solving a problem in KM
Page 169 and 170: APPENDIX A: Solving a problem in KM
Page 171: APPENDIX A: Solving a problem in KM
Page 174 and 175: 164 to learning to solve problems.
Page 176 and 177: 166 cognition in a constructivist l
Page 178 and 179: 168 forward. The most important one
Page 181 and 182: Chapter 9 SAMENVATTING Het huidige
Page 183 and 184: Samenvatting 173 De aanwezigheid va
Page 185 and 186: Samenvatting 175 gebruik van metaco
Page 187 and 188: Samenvatting 177 nificant leereffec
Page 189 and 190: References Akhras, F. and Self, J.
Page 191 and 192:
REFERENCES 181 Duffy, T. and Cunnin
Page 193 and 194:
REFERENCES 183 Nelson, T. (1999). C
Page 195:
REFERENCES 185 van Harmelen, F., Wi
Page 198 and 199:
Prototyping of CMS Storage Manageme
Page 200 and 201:
Human-Computer Interaction and Pres
Page 202:
A Model-driven Approach for Buildin
show all

The role of metacognitive skills in learning to solve problems

Create successful ePaper yourself

Delete template?

Save as template?