Rotational Raman scattering in the Earth's atmosphere ... - SRON

More documents

Recommendations

Info

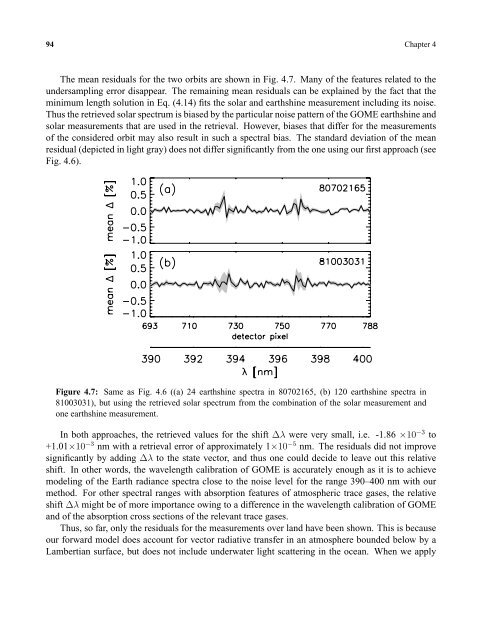
94 Chapter 4 The mean residuals for the two orbits are shown in Fig. 4.7. Many of the features related to the undersampling error disappear. The remaining mean residuals can be explained by the fact that the minimum length solution in Eq. (4.14) fits the solar and earthshine measurement including its noise. Thus the retrieved solar spectrum is biased by the particular noise pattern of the GOME earthshine and solar measurements that are used in the retrieval. However, biases that differ for the measurements of the considered orbit may also result in such a spectral bias. The standard deviation of the mean residual (depicted in light gray) does not differ significantly from the one using our first approach (see Fig. 4.6). Figure 4.7: Same as Fig. 4.6 ((a) 24 earthshine spectra in 80702165, (b) 120 earthshine spectra in 81003031), but using the retrieved solar spectrum from the combination of the solar measurement and one earthshine measurement. In both approaches, the retrieved values for the shift ∆λ were very small, i.e. -1.86 ×10 −3 to +1.01×10 −3 nm with a retrieval error of approximately 1×10 −5 nm. The residuals did not improve significantly by adding ∆λ to the state vector, and thus one could decide to leave out this relative shift. In other words, the wavelength calibration of GOME is accurately enough as it is to achieve modeling of the Earth radiance spectra close to the noise level for the range 390–400 nm with our method. For other spectral ranges with absorption features of atmospheric trace gases, the relative shift ∆λ might be of more importance owing to a difference in the wavelength calibration of GOME and of the absorption cross sections of the relevant trace gases. Thus, so far, only the residuals for the measurements over land have been shown. This is because our forward model does account for vector radiative transfer in an atmosphere bounded below by a Lambertian surface, but does not include underwater light scattering in the ocean. When we apply
Accurate modeling of spectral fine-structure in Earth radiance spectra measured with GOME 95 our model to cloud-free measurements over the ocean we obtain the mean residual shown in Fig. 4.8. Here, the solar spectrum is the same as that used in Fig. 4.7. The undersampling error is removed, but at the Ca II Fraunhofer lines almost 3% of filling in is missing. This bias can be attributed to vibrational Raman scattering in liquid water in the ocean [Vasilkov et al., 2002]. Joiner et al. [2004] presented a model that includes inelastic scattering by the ocean and showed that the extra filling in was reduced when chlorophyll was present. This was used to retrieve the chlorophyll content from the GOME measurements for cloud-free ocean scenes. Our method could be used to improve this type of retrieval that makes use of the exact shape of the Fraunhofer lines in an Earth radiance spectrum. Figure 4.8: Mean residual for 142 earthshine measurements over the ocean in orbit 80702165, using the retrieved solar spectrum from the combination of the solar measurement and one earthshine measurement over land. The light gray area corresponds to the mean residual ± 1 standard deviation. 4.6 Conclusion We have presented what we believe to be a new method that allows accurate modeling of spectral finestructure in GOME measurements without any a priori knowledge of the solar spectrum. We have presented two approaches. In our first approach, a solar spectrum was retrieved from the measured solar spectrum only. In contrast to previous work [Chance et al., 2005], our approach does not require separate knowledge of the sample and slit function; only the instrument response function needs to be known. This function is much easier to characterize than its two separate components. For the GOME instrument only the instrument response function was measured during the on-ground calibration of
Page 1 and 2:
VRIJE UNIVERSITEIT Rotational Raman
Page 5 and 6:
Contents 1 Introduction 1 1.1 Obser
Page 7 and 8:
1 Introduction 1.1 Observing skylig
Page 9 and 10:
Introduction 3 Extracting the wealt
Page 11 and 12:
Introduction 5 and Spurr, 1997, Vou
Page 13 and 14:
Introduction 7 energy: E rot (v,J)
Page 15 and 16:
Introduction 9 Figure 1.4: Probabil
Page 17 and 18:
Introduction 11 scattered radiance
Page 19 and 20:
Introduction 13 approximation in wh
Page 21 and 22:
Introduction 15 scattering have bee
Page 23 and 24:
2 A doubling-adding method to inclu
Page 25 and 26:
A doubling-adding method to include
Page 27 and 28:
Page 29 and 30:
Page 31 and 32:
Page 33 and 34:
Page 35 and 36:
Page 37 and 38:
Page 39 and 40:
Page 41 and 42:
Page 43:
Page 46 and 47:
40 Chapter 3 nm with a spectral res
Page 48 and 49:
42 Chapter 3 contributions of lower
Page 50 and 51: 44 Chapter 3 if we use the effectiv
Page 52 and 53: 46 Chapter 3 This in turn results i
Page 54 and 55: 48 Chapter 3 This may be shown in a
Page 56 and 57: 50 Chapter 3 The forward and adjoin
Page 58 and 59: 52 Chapter 3 Here, ∆ = diag [1, 1
Page 60 and 61: 54 Chapter 3 Figure 3.3: Relative R
Page 62 and 63: 56 Chapter 3 biases the simulation
Page 64 and 65: 58 Chapter 3 3.4.2 Approximation me
Page 66 and 67: 60 Chapter 3 where I ram,app and I
Page 68 and 69: 62 Chapter 3 3.5 Simulation of pola
Page 70 and 71: 64 Chapter 3 Figure 3.10: Relative
Page 72 and 73: 66 Chapter 3 dependence on the vert
Page 74 and 75: 68 Chapter 3 Figure 3.13: Same as F
Page 76 and 77: 70 Chapter 3 3.6 Summary A vector r
Page 78 and 79: 72 Chapter 3 where λ is the wavele
Page 80 and 81: 74 Chapter 3 where S l is the expan
Page 82 and 83: 76 Chapter 3 3.C Appendix: Evaluati
Page 85 and 86: 4 Accurate modeling of spectral fin
Page 87 and 88: Accurate modeling of spectral fine-
Page 99: Accurate modeling of spectral fine-
Page 103 and 104: 5 Retrieval of cloud properties fro
Page 105 and 106: Retrieval of cloud properties from
Page 125 and 126: References Aben, I., F. Helderman,
Page 127 and 128: References 121 Ellery, A., D. Wynn-
Page 129 and 130: References 123 Lacis, A. A., J. Cho
Page 131 and 132: References 125 Schulz, F., K. Stamn
Page 133 and 134: Summary A spectrum of sunlight that
Page 135 and 136: Summary 129 Earth radiance spectrum
Page 137 and 138: Samenvatting Het door de aardatmosf
Page 139 and 140: Samenvatting 133 met een vector-mod
Page 141: List of publications Peer-reviewed
show all

Rotational Raman scattering in the Earth's atmosphere ... - SRON

Create successful ePaper yourself

Delete template?

Save as template?