Rotational Raman scattering in the Earth's atmosphere ... - SRON

More documents

Recommendations

Info

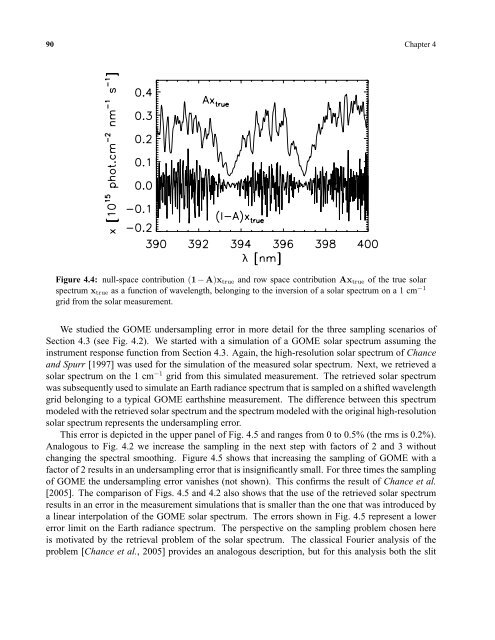
90 Chapter 4 Figure 4.4: null-space contribution (1 −A)x true and row space contribution Ax true of the true solar spectrum x true as a function of wavelength, belonging to the inversion of a solar spectrum on a 1 cm −1 grid from the solar measurement. We studied the GOME undersampling error in more detail for the three sampling scenarios of Section 4.3 (see Fig. 4.2). We started with a simulation of a GOME solar spectrum assuming the instrument response function from Section 4.3. Again, the high-resolution solar spectrum of Chance and Spurr [1997] was used for the simulation of the measured solar spectrum. Next, we retrieved a solar spectrum on the 1 cm −1 grid from this simulated measurement. The retrieved solar spectrum was subsequently used to simulate an Earth radiance spectrum that is sampled on a shifted wavelength grid belonging to a typical GOME earthshine measurement. The difference between this spectrum modeled with the retrieved solar spectrum and the spectrum modeled with the original high-resolution solar spectrum represents the undersampling error. This error is depicted in the upper panel of Fig. 4.5 and ranges from 0 to 0.5% (the rms is 0.2%). Analogous to Fig. 4.2 we increase the sampling in the next step with factors of 2 and 3 without changing the spectral smoothing. Figure 4.5 shows that increasing the sampling of GOME with a factor of 2 results in an undersampling error that is insignificantly small. For three times the sampling of GOME the undersampling error vanishes (not shown). This confirms the result of Chance et al. [2005]. The comparison of Figs. 4.5 and 4.2 also shows that the use of the retrieved solar spectrum results in an error in the measurement simulations that is smaller than the one that was introduced by a linear interpolation of the GOME solar spectrum. The errors shown in Fig. 4.5 represent a lower error limit on the Earth radiance spectrum. The perspective on the sampling problem chosen here is motivated by the retrieval problem of the solar spectrum. The classical Fourier analysis of the problem [Chance et al., 2005] provides an analogous description, but for this analysis both the slit
Accurate modeling of spectral fine-structure in Earth radiance spectra measured with GOME 91 Figure 4.5: Undersampling error in the Earth’s radiance spectrum for (a) the sampling of GOME and (b) 2× the sampling of GOME. function and the sampling function in Eq. (4.7) need to be known separately. In general, this is not the case for GOME-type spectrometers, which makes our approach particularly useful for the analysis of measurements by this type of spectrometer. Another advantage is that uneven sampling in wavelength space can be taken into account in an uncomplicated way. 4.4.3 Simulation of GOME earthshine measurements To demonstrate the use of the retrieved solar spectrum x for an accurate simulation of GOME Earth radiance spectra, we consider the measurements of two GOME orbits. The first orbit (ERS-2 orbit number 80702165) went over North America and the Pacific Ocean on 2 July, 1998, the second orbit (ERS-2 orbit number 81003031) went over Eastern Asia and the Indian Ocean on 10 October, 1998. We retrieved a solar spectrum on a 1 cm −1 grid from the direct solar measurements belonging to both orbits. Subsequently, those two spectra were used to simulate the GOME earthshine spectra in the 390–400 nm range. We restrict our study to cloud-free observations and moderate solar zenith angles, i.e. < 70 ◦ . The data were selected by using a cloud filter that was based on measurements by the polarization measurement devices of GOME [Krijger et al., 2005]. Furthermore, we determined a wavelength dependent Lambertian surface albedo from the GOME earthshine measurements by using a nonlinear least-square fitting procedure. The albedo was assumed to be linearly dependent on wavelength for the selected spectral range. This approach also accounted for the presence of aerosols in the observed scene. In addition, a wavelength shift ∆λ between the earthshine and solar spectrum was fitted in the instrument response function in Eq. (4.9) to compensate
Page 1 and 2:
VRIJE UNIVERSITEIT Rotational Raman
Page 5 and 6:
Contents 1 Introduction 1 1.1 Obser
Page 7 and 8:
1 Introduction 1.1 Observing skylig
Page 9 and 10:
Introduction 3 Extracting the wealt
Page 11 and 12:
Introduction 5 and Spurr, 1997, Vou
Page 13 and 14:
Introduction 7 energy: E rot (v,J)
Page 15 and 16:
Introduction 9 Figure 1.4: Probabil
Page 17 and 18:
Introduction 11 scattered radiance
Page 19 and 20:
Introduction 13 approximation in wh
Page 21 and 22:
Introduction 15 scattering have bee
Page 23 and 24:
2 A doubling-adding method to inclu
Page 25 and 26:
A doubling-adding method to include
Page 27 and 28:
Page 29 and 30:
Page 31 and 32:
Page 33 and 34:
Page 35 and 36:
Page 37 and 38:
Page 39 and 40:
Page 41 and 42:
Page 43:
Page 46 and 47: 40 Chapter 3 nm with a spectral res
Page 48 and 49: 42 Chapter 3 contributions of lower
Page 50 and 51: 44 Chapter 3 if we use the effectiv
Page 52 and 53: 46 Chapter 3 This in turn results i
Page 54 and 55: 48 Chapter 3 This may be shown in a
Page 56 and 57: 50 Chapter 3 The forward and adjoin
Page 58 and 59: 52 Chapter 3 Here, ∆ = diag [1, 1
Page 60 and 61: 54 Chapter 3 Figure 3.3: Relative R
Page 62 and 63: 56 Chapter 3 biases the simulation
Page 64 and 65: 58 Chapter 3 3.4.2 Approximation me
Page 66 and 67: 60 Chapter 3 where I ram,app and I
Page 68 and 69: 62 Chapter 3 3.5 Simulation of pola
Page 70 and 71: 64 Chapter 3 Figure 3.10: Relative
Page 72 and 73: 66 Chapter 3 dependence on the vert
Page 74 and 75: 68 Chapter 3 Figure 3.13: Same as F
Page 76 and 77: 70 Chapter 3 3.6 Summary A vector r
Page 78 and 79: 72 Chapter 3 where λ is the wavele
Page 80 and 81: 74 Chapter 3 where S l is the expan
Page 82 and 83: 76 Chapter 3 3.C Appendix: Evaluati
Page 85 and 86: 4 Accurate modeling of spectral fin
Page 87 and 88: Accurate modeling of spectral fine-
Page 95: Accurate modeling of spectral fine-
Page 103 and 104: 5 Retrieval of cloud properties fro
Page 105 and 106: Retrieval of cloud properties from
Page 125 and 126: References Aben, I., F. Helderman,
Page 127 and 128: References 121 Ellery, A., D. Wynn-
Page 129 and 130: References 123 Lacis, A. A., J. Cho
Page 131 and 132: References 125 Schulz, F., K. Stamn
Page 133 and 134: Summary A spectrum of sunlight that
Page 135 and 136: Summary 129 Earth radiance spectrum
Page 137 and 138: Samenvatting Het door de aardatmosf
Page 139 and 140: Samenvatting 133 met een vector-mod
Page 141: List of publications Peer-reviewed
show all

Rotational Raman scattering in the Earth's atmosphere ... - SRON

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?