FIBEROPTIC SENSOR TECHNOLOGY HANDBOOK

in the right center of Fig. 2.13. They increase in
magnitude from zero along the axis of the core to a
maximum and then decay as the core-cladding interface
is approached, as shown in the lower right. As already
pointed out for the HE1l mode in this case, the fields
again extend beyond the core into the cladding.
Returning to the graph at the left in Fig.
2.13, as V is increased further, for example by decreasing
the wavelength, ,10, of the light injected into
the fiber, additional relatively lossless modes are permitted
and, very rapidly, propagation phenomena change
from the single or few mode types to multimode behavior.
In fact, for V > 10 the number of allowed modes is approximately
equal to V2/2 for a step-index fiber. As
already pointed out above in the discussion of the radial
electric field distribution for the HE1l and TEOl
modes, shown in the lower right in Fig. 2.12 and 2.13,
respectively, the ~-fields may extend well beyond the
core cladding interface. In fact when each mode is
first allowed much of its energy is associated with
fields that penetrate the cladding. This phenomena is
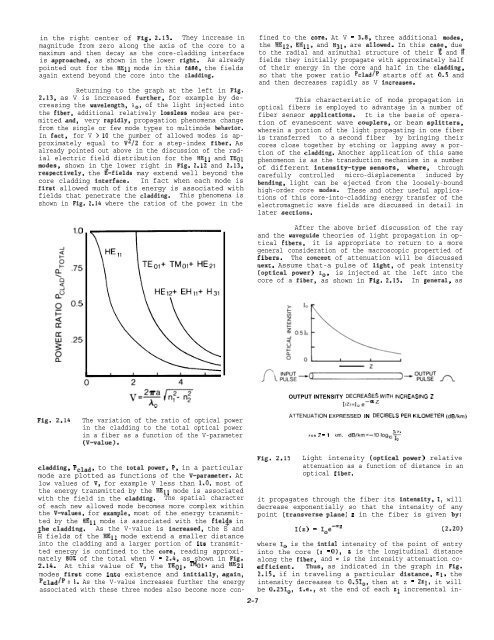
shown in Fig. 2.14 where the ratios of the power in the
cladding, pclad, to the total power, F’, in a particular
mode are plotted as functions of the V-parameter. At
low values of V, for example V less than 1.0, most of
the energy transmitted by the HE1l mode is associated
with the field in the cladding. The spatial character
of each new allowed mode becomes more complex within
the V-values, for example, most of the energy transmitted
by the HE1l mode is associated with the fiel~s in
$he cladding. As the V-value is increased, the E and
H fields of the HE1l mode extend a smaller distance
into the cladding and a larger portion of its transmitted
energy is confined to the core, reading approximately
80% of the total when V = 2.4, as shown in Fig.
2.14. At this value of V, the TEOl, TMOl, and HE21
modes first come into existence and initially, again,
pcladtpz 1. As the V-value increases further the energy
associated with these three modes also become more confined
to the core. At V = 3.8, three additional modes,
the HE12, EH1l, and H31, are allowed. In this case, due
to the radial and azimuthal structure of their ~ and P
fields they initially propagate with approximately half
of their energy in the core and half in the cladding,
so that the power ratio Pclad/P starts off at 0.5 and
and then decreases rapidly as V increases.
This characteristic of mode propagation in
optical fibers is employed to advantage in a number of
fiber sensor applications. It is the basis of operation
of evanescent wave couplers, or beam splitters,
wherein a portion of the light propagating in one fiber
is transferred to a second fiber by bringing their
cores close together by etching or lapping away a portion
of the cladding. Another application of this same
phenomenon is as the transduction mechanism in a number
of different intenaity-type aensors, where, through
carefully controlled micro-displacements induced by
bending, light can be ejected from the loosely-bound
high-order core modes. These and other useful applications
of this core-into-cladding energy transfer of the
electromagnetic wave fields are discussed in detail in
later sections.
After the above brief discussion of the ray
and the waveguide theories of light propagation in optical
fibers, it is appropriate to return to a more
general consideration of the macroscopic propertied of
fibers. The conceut of attenuation will be discussed
next. Assume that-a pulse of light, of peak intensity
(optical power) 1., is injected at the left into the
core of a fiber, as shown in Fig. 2.15. In general, as
OUTPUT INTENSITY DECREASES WI’H INCREASING
IIZ)=Ioe–az
Fig. 2.14 The variation of the ratio of optical power
in the cladding to the total optical power
in a fiber as a function of the V-parameter
(V-value).
ATTENUATION EXPRESSED IN DECIBELS PER KILOMETER (dB/km)
I(z)
FOR Z . 1 km, dB/km=–lOloglo~
2-7
Fig. 2.15 Light intensity (optical power) relative
attenuation as a function of distance in an
optical fiber.
it propagates through the fiber its intensity, I, will
decrease exponentially so that the intensity of any
point (transverse plane) z in the fiber is given by:
I(z) = Ioe-az (2.20)
where 10 is the intial intensity of the point of entry
into the core (z = O), z is the longitudinal distance
along the fiber, and = is the intensity attenuation coefficient.
Thus, as indicated in the graph in Fig.
2.15, if in traveling a particular distance, z1, the
intensity decreases to 0.51., then at z = 2z1, it will
be 0.251., i.e., at the end of each Z1 incremental in-