The Quick Count and Election Observation

CHAPTER FIVE: STATISTICAL PRINCIPLES AND QUICK COUNTS
68 The formula, then, is as follows:
For a dataset containing observations x 1
, x 2
, x 3
… x n
s 2 = (x 1 -x)2 + (x 2 -x) 2 + (x 3 -x) 2 ... (x n -x) 2
n-1
Where
s 2 = variance
x 1
, x 2
, x 3
… x n
are the observations
x is the mean
n is the number of observations
In short form, it appears as:
s 2 =
∑ (x-x)2
n-1
The standard deviation is the square root of the variance. Statisticians usually
rely on the standard deviation because it expresses the variance in standardized
units that can be meaningfully compared. The larger the standard deviation
for any dataset, the more the data are spread out from the mean. The smaller
the standard deviation, the more tightly are the individual data points
clustered around the mean.
There is one additional measurement concept that needs to be considered: the
normal distribution. The preceding discussion shows that, in every data set, individual
data points will cluster around an average, or mean, point. Another way
to express the same idea is to consider what proportion of all of the observations
fall within one standard deviation of the mean. If datasets are large enough,
and if they conform to the principles of randomness, the dispersion of the data
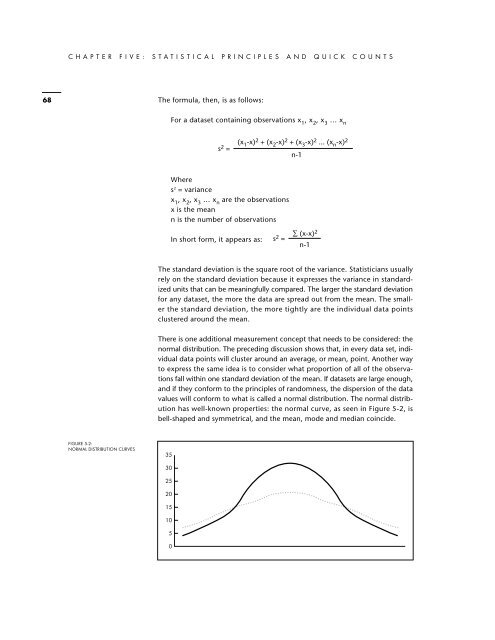
values will conform to what is called a normal distribution. The normal distribution
has well-known properties: the normal curve, as seen in Figure 5-2, is
bell-shaped and symmetrical, and the mean, mode and median coincide.
FIGURE 5-2:
NORMAL DISTRIBUTION CURVES
35
30
25
20
15
10
5
0