Biomass Feasibility Project Final Report - Xcel Energy

MULTIPLE VARIABLE SENSITIVITY ANALYSIS (MONTE CARLO)
BioPet performs one type of sensitivity analysis, allowing the user to see how variations in a single
selected parameter affect outcomes. We also used Monte Carlo techniques to analyze the
effects of several variable assumptions jointly.
The single value assigned to each assumption/parameter may not always reflect the true
condition of the system we are examining. We know all variables with imprecision. In some
cases such as crop yields, the variability is due to stochastic events like climate. In other cases,
such as local production participation rates, we simply are ignorant of the “true” value of the
factor. But in every case, we can assign a probability density function which describes our prior
expectation of each factor’s variability.
The key feature of the Monte Carlo analysis is repetition. Because we don’t know the single
“true” value of certain factors, but only the distribution of the probability for that value (assigned
by us), we can’t simply run the model once and then report the result. Instead, we run the
model over and over, each time sampling from the parameter distributions, according to the
stated form of the distribution. In a given run we might draw from the upper end of one
parameter’s distribution and the mid-point of another’s. In the next run, the draw might be
opposite. And so on, for hundreds or thousands of runs.
For each run, we record the outcomes of the model for that run’s parameter sample selections.
Each new set of parameter values yields a different outcome. After hundreds or thousands of
runs, we obtain a distribution of outcome estimates. This can be interpreted as the spread of
possible outcomes given the stated distributions of the variable assumption. A wide range
suggests that we should be very careful about too quickly adopting the single-value outcome of
the initial parameters. Too, we can compare among scenarios to see if some have narrower
outcome ranges than to others, or if some clearly “outperform” others despite a wide range of
parameter uncertainty.
The Monte Carlo simulations were performed using feedstock and power plant templates
generated with the BioPET software tool. Most of the variables were generated using the default
values within BioPET. For those variables which would be varied within the Monte Carlo
Simulation the mean value of the variable’s range was used as a default. Some of the Monte
Carlo variables are market or processing costs which have considerable variability. In those
cases the mean value is somewhat different than the default value due to fact that the default
values were chosen to be representative of current prices as opposed to average long term
prices.
These templates include all costs incurred to deliver fuel to the power plant. Any processing
costs at the power plant are included in the operating costs of the plant. Four power plant
templates were generated. The templates are derived from publicly available documents. Two
of the templates are derived from engineering and financial studies of specific projects. The
others are derived from more general documents that have contained information on power
plant costs.
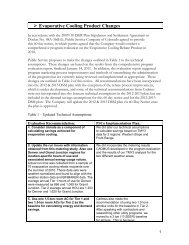
Power Plant Assumptions
The source documents for each of the power plant templates use somewhat different financial
and operating assumptions. For the purposes of the Monte Carlo simulations a number of
uniform assumptions were utilized to provide a degree of standardization across power plants. A
uniform mean capacity factor of 85% was utilized for each power plant template. All other
Page 128
Identifying Effective Biomass Strategies:
Quantifying Minnesota’s Resources and Evaluating Future Opportunities