Violation in Mixing

104 Strategy and Tools for Charmless Two-body � Decays Analysis
Events/2.5 MeV/c 2
150
100
50
BABAR
mES(D 0 0
5.22 5.24 5.26 5.28 5.3
π)
Events/10 MeV/c 2
100
50
0
BABAR
ΔE(D 0 -0.1 0 0.1
π)
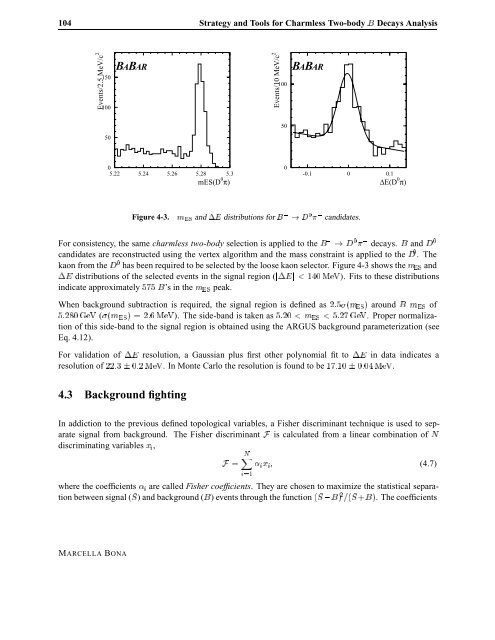
Figure 4-3. Ñ�Ë and ¡� distributions for � � � � candidates.
For consistency, the same charmless two-body selection is applied to the � � � � decays. � and �
candidates are reconstructed using the vertex algorithm and the mass constraint is applied to the � . The
kaon from the � has been required to be selected by the loose kaon selector. Figure 4-3 shows the Ñ�Ë and
¡� distributions of the selected events in the signal region (�¡�� � � Å�Î). Fits to these distributions
indicate approximately ��� �’s in the Ñ�Ë peak.
When background subtraction is required, the signal region is defined as ��� Ñ�Ë around � Ñ�Ë of
�� � ��Î (� Ñ�Ë � ��Å�Î). The side-band is taken as �� �Ñ�Ë � �� � ��Î. Proper normalization
of this side-band to the signal region is obtained using the ARGUS background parameterization (see
Eq. 4.12).
For validation of ¡� resolution, a Gaussian plus first other polynomial fit to ¡� in data indicates a
resolution of � ¦ � Å�Î. In Monte Carlo the resolution is found to be �� ¦ � � Å�Î.
4.3 Background fighting
In addiction to the previous defined topological variables, a Fisher discriminant technique is used to separate
signal from background. The Fisher discriminant � is calculated from a linear combination of Æ
discriminating variables �,
� �
�
��
«�Ü�� (4.7)
where the coefficients «� are called Fisher coefficients. They are chosen to maximize the statistical separation
between signal (Ë) and background (�) events through the function Ë � � Ë � . The coefficients
MARCELLA BONA