Violation in Mixing

2.2 The BABAR detector. 67
entries per 5 MeV/c 2
x 10 2
1500
1000
500
Without DIRC
With DIRC
0
1.75 1.8 1.85 1.9 1.95
Kπ mass (GeV/c 2 )
Kaon Efficiency
π Mis-ID as K
1
0.9
0.8
0.7
0.6
0.2
0.1
0
1 2 3
Track Momentum (GeV/c)
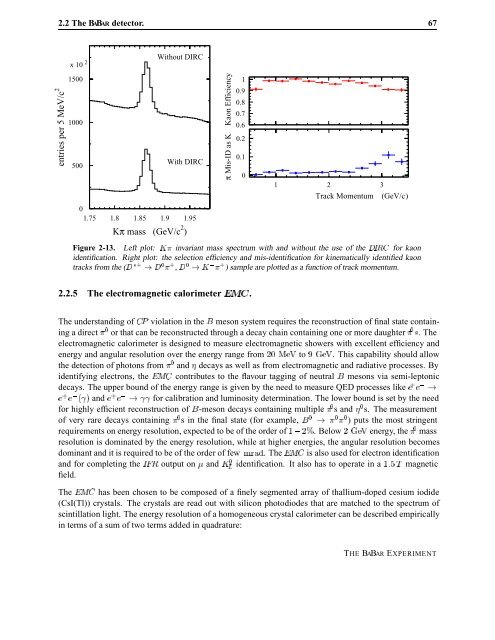
Figure 2-13. Left plot: Ã� invariant mass spectrum with and without the use of the �ÁÊ� for kaon
identification. Right plot: the selection efficiency and mis-identification for kinematically identified kaon
tracks from the (� £ � � � , � � Ã � ) sample are plotted as a function of track momentum.
2.2.5 The electromagnetic calorimeter ��.
The understanding of �È violation in the � meson system requires the reconstruction of final state containing
a direct � or that can be reconstructed through a decay chain containing one or more daughter � ×. The
electromagnetic calorimeter is designed to measure electromagnetic showers with excellent efficiency and
energy and angular resolution over the energy range from Å�Î to ���Î. This capability should allow
the detection of photons from � and � decays as well as from electromagnetic and radiative processes. By
identifying electrons, the �� contributes to the flavour tagging of neutral � mesons via semi-leptonic
decays. The upper bound of the energy range is given by the need to measure QED processes like � � �
� � ­ and � � � ­­ for calibration and luminosity determination. The lower bound is set by the need
for highly efficient reconstruction of �-meson decays containing multiple � s and � s. The measurement
of very rare decays containing � s in the final state (for example, � � � � ) puts the most stringent
requirements on energy resolution, expected to be of the order of . Below ��Îenergy, the � mass
resolution is dominated by the energy resolution, while at higher energies, the angular resolution becomes
dominant and it is required to be of the order of few ÑÖ��. The �Å� is also used for electron identification
and for completing the Á�Ê output on � and Ã Ä identification. It also has to operate in a �� Ì magnetic
field.
The �� has been chosen to be composed of a finely segmented array of thallium-doped cesium iodide
(CsI(Tl)) crystals. The crystals are read out with silicon photodiodes that are matched to the spectrum of
scintillation light. The energy resolution of a homogeneous crystal calorimeter can be described empirically
in terms of a sum of two terms added in quadrature:
THE BABAR EXPERIMENT