Violation in Mixing

3.3 Studies on data 83
0.504
0.502
0.5
0.498
0.496
0.494
observed Ks candidate masses
0.492
0 0.5 1 1.5 2 2.5 3
ks daughter theta angle
0.008
0.007
0.006
0.005
0.004
0.003
0.002
0.001
observed Ks candidate mass resolution
0
0 0.5 1 1.5 2 2.5 3
ks daughter theta angle
0.504
0.502
0.5
0.498
0.496
0.494
observed Ks candidate masses
0.492
0 0.5 1 1.5 2 2.5 3
ks daughter theta angle
0.008
0.007
0.006
0.005
0.004
0.003
0.002
0.001
observed Ks candidate mass resolution
0
0 0.5 1 1.5 2 2.5 3
ks daughter theta angle
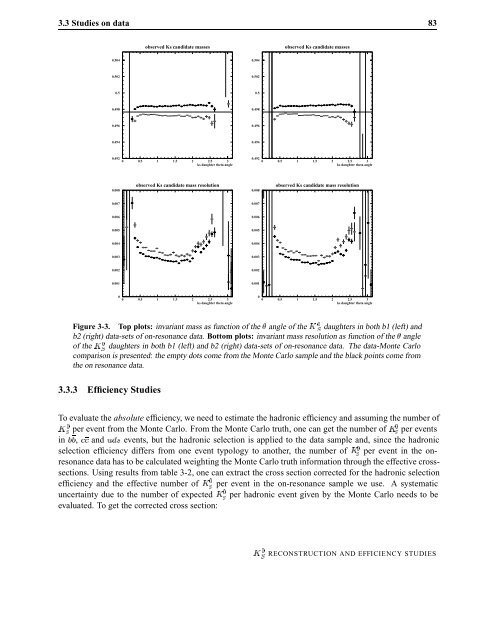
Figure 3-3. Top plots: invariant mass as function of the � angle of the Ã Ë daughters in both b1 (left) and
b2 (right) data-sets of on-resonance data. Bottom plots: invariant mass resolution as function of the � angle
of the Ã Ë daughters in both b1 (left) and b2 (right) data-sets of on-resonance data. The data-Monte Carlo
comparison is presented: the empty dots come from the Monte Carlo sample and the black points come from
the on resonance data.
3.3.3 Efficiency Studies
To evaluate the absolute efficiency, we need to estimate the hadronic efficiency and assuming the number of
Ã Ë per event from the Monte Carlo. From the Monte Carlo truth, one can get the number of Ã Ë per events
in ��, and Ù�× events, but the hadronic selection is applied to the data sample and, since the hadronic
selection efficiency differs from one event typology to another, the number of Ã Ë per event in the onresonance
data has to be calculated weighting the Monte Carlo truth information through the effective crosssections.
Using results from table 3-2, one can extract the cross section corrected for the hadronic selection
efficiency and the effective number of Ã Ë per event in the on-resonance sample we use. A systematic
uncertainty due to the number of expected Ã Ë per hadronic event given by the Monte Carlo needs to be
evaluated. To get the corrected cross section:
Ã Ë RECONSTRUCTION AND EFFICIENCY STUDIES