Beispiele mechatronischer Systeme
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
9.2 Funktionsentwicklung und Applikation in der MSG-Entwicklung xvii<br />
Das dynamische Verhalten des gesamten Antriebsstrangs lässt sich im Zeitbereich kompakt<br />
und einheitlich in der Zustandsraumdarstellung gemäß Abschnitt 7.1.2 beschreiben. Dadurch<br />
wird nicht nur das Ein-/Ausgangsverhalten abgebildet, sondern darüber hinaus ist der Zugriff<br />
auf interne Vorgänge des Systems möglich, womit wiederum ein zusätzlicher Modellabgleich<br />
durchgeführt werden kann. Das System des Zweimassenschwingers besitzt mit einer Feder<br />
und zwei rein rotatorischen Massen insgesamt drei Energiespeicher, so dass nach Seite 257<br />
drei Zustände für die Formulierung der Antriebsstrangdynamik im Zustandsraum notwendig<br />
sind. Für die Wahl des Zustandsvektors x bieten sich die Motorgeschwindigkeit ˙ϕ m und die<br />
Radgeschwindigkeit ˙ϕ r an, da sie direkt gemessen werden können. Als weiterer Zustand wird<br />
der relative Verdrehwinkel τ= ϕ m<br />
i<br />
−ϕ r zwischen Motor- und Radmasse unter Berücksichtigung<br />
der Getriebeübersetzung i gewählt:<br />
x T = [ τ, ˙ϕ m , ˙ϕ r<br />
]<br />
. (9.14)<br />
Für die Zustandsraumdarstellung des Zweimassenschwingermodells ergibt sich für die Systemmatrix<br />
A und Eingangsmatrix B mit dem gewählten Zustandsvektor x die nachfolgende<br />
Darstellung. Die Mess- bzw. Ausgangsmatrix C und die Durchgangsmatrix D bestimmen den<br />
Ausgangsvektor y,<br />
⎡<br />
A= ⎢<br />
⎣<br />
0<br />
− c a<br />
i J 1<br />
c a<br />
J2<br />
1<br />
i<br />
− b 1i 2 +d a<br />
i 2 J 1<br />
d a<br />
i J 2<br />
−1<br />
d a<br />
⎥<br />
i J 1 ⎦ ,<br />
⎤<br />
− d a<br />
J 2<br />
⎡<br />
0 0 ⎡ ⎤<br />
B = ⎢<br />
1<br />
⎣ J 1<br />
0 ⎥<br />
⎦ und C = ⎣ 0 1 0 ⎦ . (9.15)<br />
0 0 1<br />
1<br />
0<br />
Da das System keinen direkten Durchgriff besitzt, gilt D = 0. Der Eingangsvektor setzt sich aus<br />
den motor- und den radseitigen Momenten zusammen<br />
u T = [ M mot , −M rad<br />
]<br />
.<br />
J 2<br />
⎤<br />
Drehzahl [1/min]<br />
2200<br />
2000<br />
1800<br />
1600<br />
1400<br />
Messung<br />
Modell<br />
0 2 4 6 8<br />
Zeit [s]<br />
Geschwindigkeit [km/h]<br />
32<br />
30<br />
28<br />
26<br />
24<br />
0 2 4 6 8<br />
Zeit [s]<br />
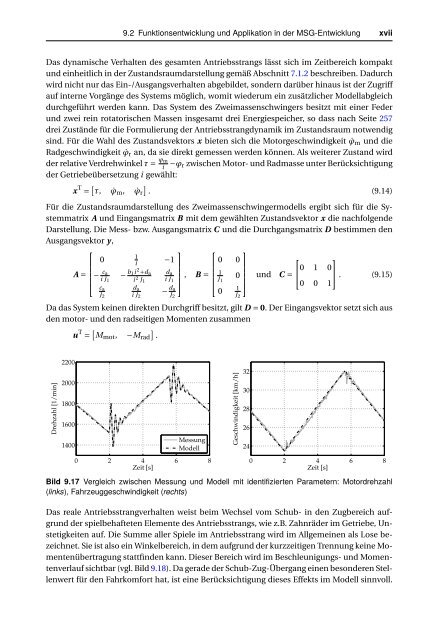
Bild 9.17 Vergleich zwischen Messung und Modell mit identifizierten Parametern: Motordrehzahl<br />
(links), Fahrzeuggeschwindigkeit (rechts)<br />
Das reale Antriebsstrangverhalten weist beim Wechsel vom Schub- in den Zugbereich aufgrund<br />
der spielbehafteten Elemente des Antriebsstrangs, wie z.B. Zahnräder im Getriebe, Unstetigkeiten<br />
auf. Die Summe aller Spiele im Antriebsstrang wird im Allgemeinen als Lose bezeichnet.<br />
Sie ist also ein Winkelbereich, in dem aufgrund der kurzzeitigen Trennung keine Momentenübertragung<br />
stattfinden kann. Dieser Bereich wird im Beschleunigungs- und Momentenverlauf<br />
sichtbar (vgl. Bild 9.18). Da gerade der Schub-Zug-Übergang einen besonderen Stellenwert<br />
für den Fahrkomfort hat, ist eine Berücksichtigung dieses Effekts im Modell sinnvoll.