Beispiele mechatronischer Systeme

9.6 Inertiale Stabilisierung einer Lastkarre mit Momentenkreiseln lxi
In Matrixdarstellung lauten die Systembeschreibung mit der Systemmatrix A und dem Steuervektor
b
⎡ ⎤ ⎡
˙ψ
¨ψ
ẋ = ⎢ ⎥
⎣ ˙ϕ P ⎦ = ⎢
⎣
¨ϕ P
⎤⎡
⎤ ⎡
0 1 0 0 ψ
m G g l P
J
− d 2 J
P J
0 G ω
P J P
˙ψ
⎥⎢
⎥+
⎢
0 0 0 1 ⎦⎣ϕ P ⎦ ⎣
0 0 0 − 1 ˙ϕ
T P
} {{ 1
}} {{ }
A
x
wofür man nun einen Zustandsregler
⎤
0
0
⎥
0 ⎦
1
T 1
} {{ }
b
ω soll
P
}{{}
u
, (9.89)
u= ω soll
P
=−k T x , (9.90)
z. B. per Polzuweisung (Abschnitt 8.3) oder mittels Optimierung eines quadratischen Gütemaßes
(Abschnitt 8.4.1) entwerfen kann. Hier ist kein Beobachter erforderlich, da alle Zustände
vorliegen. Der Nickwinkel ψ und die Nickrate ˙ψ kommen direkt aus der IMU M6-LT, die ihrerseits
intern ein Extended KALMAN-Filter implementiert. Den Präzessionswinkel ϕ P erfasst ein
HALL-Encoder mit 14 Bit Auflösung hinreichend genau und die Präzessionsgeschwindigkeit
˙ϕ P folgt aus einer numerischen Differentiation.
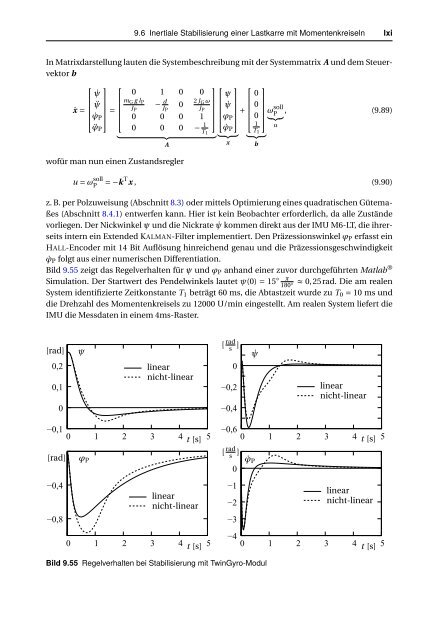
Bild 9.55 zeigt das Regelverhalten für ψ und ϕ P anhand einer zuvor durchgeführten Matlab ®
Simulation. Der Startwert des Pendelwinkels lautet ψ(0) = 15 ◦ π
180 ◦ ≈ 0,25rad. Die am realen
System identifizierte Zeitkonstante T 1 beträgt 60 ms, die Abtastzeit wurde zu T 0 = 10 ms und
die Drehzahl des Momentenkreisels zu 12000 U/min eingestellt. Am realen System liefert die
IMU die Messdaten in einem 4ms-Raster.
[rad]
ψ
[ rad
s ] ˙ψ
0,2
0,1
0
linear
nicht-linear
0
−0,2
−0,4
linear
nicht-linear
−0,1
0
[rad]
ϕ P
1
2
3
4 t [s]
5
−0,6
0
[ rad
0
˙ϕ P
1
2
3
4
t [s]
5
s ]
t [s]
−0,4
−0,8
linear
nicht-linear
−1
−2
−3
linear
nicht-linear
0
1
2
3
4
t [s]
5
−4
0
1
2
3
4
5
Bild 9.55 Regelverhalten bei Stabilisierung mit TwinGyro-Modul