full Paper - Nguyen Dang Binh

formula, instead of a system of differential equations. The
steering wheel simplified model calculates the torque τ at
the steering wheel as a function of the vehicle longitudinal
velocity Vx and the steering wheel angular displacement δw.
The approach proposed in this section has been validated by
experimental data collected for a FIAT PUNTO. The steering
wheel torque can be split into different terms to clearly
show the physical meaning of the equation:
τ τi ¨ δw τ0 Ay τ1 Vx ˙ δw τ2 ˙ δw τ3 ˙ δw (1)
The term τi is the inertial torque. Knowing the steering
wheel moment of inertia Jw, the value of τi is:
τi ¨ δw Jw ¨ δw (2)
The term τ0 is the torque due to the vehicle lateral acceleration
Ay, which has been derived from the linear timeinvariant
bicycle model. However, since it is not correct to
consider that the vehicle behaviour is linear in every condition,
so the lateral acceleration of the bicycle model Ayb
has been adjusted to fit with experimental data. The relation
between the Ay and Ayb derived from the bicycle model is:
Ay K ¡ max Ay ¡tan
1 Ayb
K0
On the basis of equation 3, the expression of τ0 determined
by interpolation of track data acquisition is:
τ0
K1Ay
1 K2A K3
y
The term τ1 is the torque due to the tire spin. The parameter
that most influences this torque is the vehicle longitudinal
velocity Vx. In order to have the torque sense and avoid discontinuity,
the steering wheel angular velocity is also taken
into account in the following equation:
1
τ1
K4 K5Vx
¡tan 1 ˙ δw
K6
The term τ2 is the torque due to the friction present in all
the steering system:
τ2 K7 ¡tan 1 ˙ δw
K8
The term τ3 represents the damping contribute:
τ3 K9 ˙ δw
To sum up, some comparisons between the values of the
steering wheel torque, calculated with the proposed method,
and the experimental data, collected on the track for an FIAT
PUNTO, are represented below. Different kinds of manoeuvres
have been used for the model validation: "steady state"
Massimo Bergamasco / Crating haptic response
(3)
(4)
(5)
(6)
(7)
39
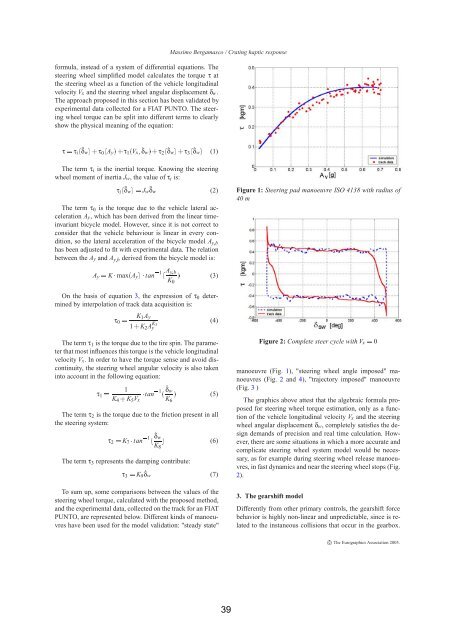
Figure 1: Steering pad manoeuvre ISO 4138 with radius of
40 m
Figure 2: Complete steer cycle with Vx 0
manoeuvre (Fig. 1), "steering wheel angle imposed" manoeuvres
(Fig. 2 and 4), "trajectory imposed" manoeuvre
(Fig. 3 )
The graphics above attest that the algebraic formula proposed
for steering wheel torque estimation, only as a function
of the vehicle longitudinal velocity Vx and the steering
wheel angular displacement δw, completely satisfies the design
demands of precision and real time calculation. However,
there are some situations in which a more accurate and
complicate steering wheel system model would be necessary,
as for example during steering wheel release manoeuvres,
in fast dynamics and near the steering wheel stops (Fig.
2).
3. The gearshift model
Differently from other primary controls, the gearshift force
behavior is highly non-linear and unpredictable, since is related
to the instaneous collisions that occur in the gearbox.
c­ The Eurographics Association 2005.