programming with max/msp - Virtual Sound

More documents

Recommendations

Info

LEARNING AGENDA 2T PREREQUISITES FOR THE CHAPTER • Contents of Chapter 1 (theory) LEARNING OBJECTIVES Knowledge • to learn about the theory behind adding waveforms (phase, ConstruCtive interferenCe, destruCtive interferenCe) • to learn about the theory and use of basiC additive synthesis, using both fixed and variable speCtra to produCe both harmoniC and non-harmoniC sounds • to learn about the relationship between phase and beats • to learn how to use wavetables, and how interpolation is implemented • to learn some theory to support basiC veCtor synthesis SKillS • to be able to differentiate between harmoniC and non-harmoniC sounds • to be able to reCognize beats upon hearing them • to identify the different segments of a sound envelope, and to desCribe their CharaCteristiCs CONTENTS • additive synthesis using both fixed and variable speCtra • harmoniC and non-harmoniC sounds • phase and beats • interpolation • veCtor synthesis ACTIVITIES • interaCtive examples TESTING • Questions with short answers • listening and analysis SUPPORTING MATERIALS • fundamental ConCepts • glossary • disCography from “Electronic Music and Sound Design” Vol. 1 by Alessandro Cipriani and Maurizio Giri © ConTempoNet 2010 - All rights reserved
Chapter 2T - Additive and vector synthesis 2.1 FIXED SPECTRUM ADDITIVE SYNTHESIS A sound produced by an acoustic instrument, any sound at all, is a set of complex oscillations, all produced simultaneously by the instrument in question. Each oscillation contributes a piece of the overall timbre of the sound, and their sum wholly determines the resulting waveform. However, this summed set of oscillations, this complex waveform, can also be described as a group of more elementary vibrations: sine waves. Sine waves are the basic building blocks with which it is possible to construct all other waveforms. When used in this way, we call the sine waves frequency components, and each frequency component in the composite wave has its own frequency, amplitude, and phase. The set of frequencies, amplitudes, and phases that completely define a given sound is called its sound spectrum. Any sound, natural or synthesized, can be decomposed into a group of frequency components. Synthesized waveforms such as we described in Section 1.2 are no exception; each has its own unique sound spectrum, and can be built up from a mixture of sine waves. (Sine waves themselves are self-describing – they contain only themselves as components!). SPECTRUM AND WAVEFORM Spectrum and waveform are two different ways to describe a single sound. Waveform is the graphical representation of amplitude as a function of time. 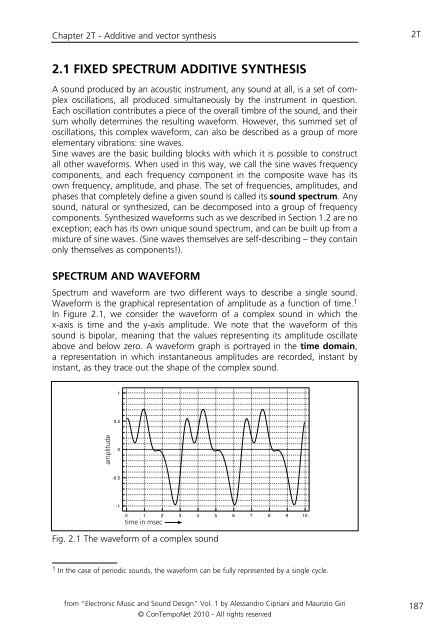1 In Figure 2.1, we consider the waveform of a complex sound in which the x-axis is time and the y-axis amplitude. We note that the waveform of this sound is bipolar, meaning that the values representing its amplitude oscillate above and below zero. A waveform graph is portrayed in the time domain, a representation in which instantaneous amplitudes are recorded, instant by instant, as they trace out the shape of the complex sound. amplitude � �� time in msec Fig. 2.1 The waveform of a complex sound 1 In the case of periodic sounds, the waveform can be fully represented by a single cycle. from “Electronic Music and Sound Design” Vol. 1 by Alessandro Cipriani and Maurizio Giri © ConTempoNet 2010 - All rights reserved 2T 187
Page 1 and 2:
Alessandro Cipriani • Maurizio Gi
Page 3 and 4:
Alessandro Cipriani • Maurizio Gi
Page 5 and 6:
CONTENTS Foreword by David Zicarell
Page 7 and 8:
Electronic Music and Sound Design -
Page 9 and 10:
Page 11 and 12:
Page 13 and 14:
Page 15 and 16: Electronic Music and Sound Design -
Page 17 and 18: LEARNING AGENDA 1T PREREQUISITES FO
Page 19 and 20: 1.1 4 Theory sound or sounds that w
Page 21 and 22: 1.1 6 Theory ��
Page 23 and 24: 1.2 8 Theory Let’s look at a tabl
Page 25 and 26: 1.2 10 Theory time (by measuring th
Page 27 and 28: 1.2 12 Theory By the same reasoning
Page 29 and 30: 1.2 14 Theory If the amplitude of a
Page 31 and 32: 1.2 16 Theory 8 140 the threshold o
Page 33 and 34: 1.2 18 Theory 1000 Hz was chosen as
Page 35 and 36: LEARNING AGENDA 1P PREREQUISITES FO
Page 37 and 38: 1.1 52 Practice Paragraph 1.1 - Fir
Page 53 and 54: 1.2 68 Practice Paragraph 1.2 - Fre
Page 55 and 56: Interlude A PROGRAMMING WITH MAX/MS
Page 57 and 58: Interlude A - Programming with Max/
Page 65: 2T ADDITIVE AND VECTOR SYNTHESIS 2.
Page 69 and 70: Chapter 2T - Additive and vector sy
Page 71 and 72: Chapter 2T - Additive and vector sy
Page 73 and 74: 2P ADDITIVE AND VECTOR SYNTHESIS 2.
Page 75 and 76: Chapter 2P - Additive and vector sy
Page 85 and 86: 3.1 296 Theory dB Fig. 3.1 The spec
Page 87 and 88: 3.1 298 Theory Paragraph 3.1 - Soun
Page 89 and 90: 3.2 300 Theory Paragraph 3.2 - Lowp
Page 91 and 92: LEARNING AGENDA 3P PREREQUISITES FO
Page 93 and 94: 3.1 358 Practice Make sure to try s
Page 95 and 96: 3.1 360 Practice Fig. 3.6 The rand~
Page 97 and 98: 3.2 362 Practice Paragraph 3.2 - Lo
Page 99 and 100: LEARNING AGENDA IB PREREQUISITES FO
Page 101 and 102: IB1 424 Practice defined to be the
Page 103 and 104: IB2 426 Practice From this example,
Page 107 and 108: 4.2 474 Theory In the example, the
Page 109 and 110: 4P CONTROL SIGNALS 4.1 CONTROL SIGN
Page 111 and 112: Chapter 4P - Control signals 4.1 CO
Page 113 and 114: Chapter 4P - Control signals Under
Page 115 and 116: REFERENCES The decision was made to
Page 117 and 118:
528 constructive interference, 190,
Page 119 and 120:
530 multislider, 164, 179 multislid
Page 121 and 122:
532 switch, 434, 468 T t (see trigg
show all

programming with max/msp - Virtual Sound

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?