diss_SCHWAIGER.pdf - OPUS Bayreuth - Universität Bayreuth

5.3 Verteilungsfunktion des MSD für zweidimensionale Zufallsbewegungen
4
70
60
3
50
Wahrscheinlichkeit
2
Wahrscheinlichkeit
40
30
1
20
10
0
-0.4 -0.2 0 0.2 0.4
Verschiebung / µm
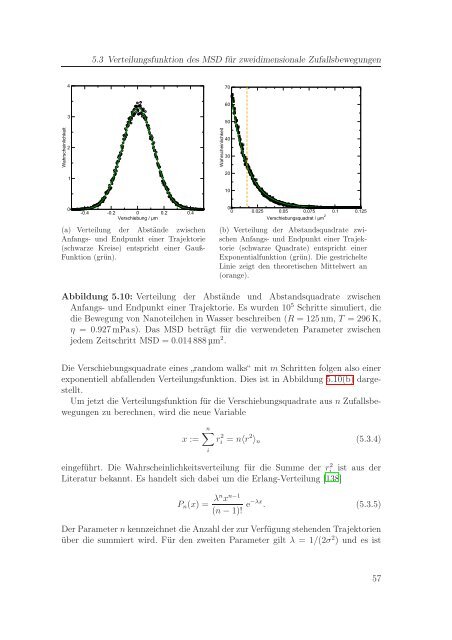
(a) Verteilung der Abstände zwischen
Anfangs- und Endpunkt einer Trajektorie
(schwarze Kreise) entspricht einer Gauß-
Funktion (grün).
0
0 0.025 0.05 0.075 0.1 0.125
Verschiebungsquadrat / µm 2
(b) Verteilung der Abstandsquadrate zwischen
Anfangs- und Endpunkt einer Trajektorie
(schwarze Quadrate) entspricht einer
Exponentialfunktion (grün). Die gestrichelte
Linie zeigt den theoretischen Mittelwert an
(orange).
Abbildung 5.10: Verteilung der Abstände und Abstandsquadrate zwischen
Anfangs- und Endpunkt einer Trajektorie. Es wurden 10 5 Schritte simuliert, die
die Bewegung von Nanoteilchen in Wasser beschreiben (R = 125 nm, T = 296 K,
η = 0.927 mPas). Das MSD beträgt für die verwendeten Parameter zwischen
jedem Zeitschritt MSD = 0.014888µm 2 .
Die Verschiebungsquadrate eines „random walks“ mit m Schritten folgen also einer
exponentiell abfallenden Verteilungsfunktion. Dies ist in Abbildung 5.10(b) dargestellt.
Um jetzt die Verteilungsfunktion für die Verschiebungsquadrate aus n Zufallsbewegungen
zu berechnen, wird die neue Variable
x :=
n∑
ri 2 = n〈r 2 〉 n (5.3.4)
i
eingeführt. Die Wahrscheinlichkeitsverteilung für die Summe der r 2 i ist aus der
Literatur bekannt. Es handelt sich dabei um die Erlang-Verteilung [138]
P n (x) = λn x n−1
(n−1)! e−λx . (5.3.5)
Der Parameternkennzeichnet die Anzahl der zur Verfügung stehenden Trajektorien
über die summiert wird. Für den zweiten Parameter gilt λ = 1/(2σ 2 ) und es ist
57