Coherent Backscattering from Multiple Scattering Systems - KOPS ...

2 Theory
45
ellipticity / azimuth [deg]
30
15
0
−15
−30
azimuth ellipticity
−45
−180 −135 −90 −45 0 45 90 135 180
scattering angle [deg]
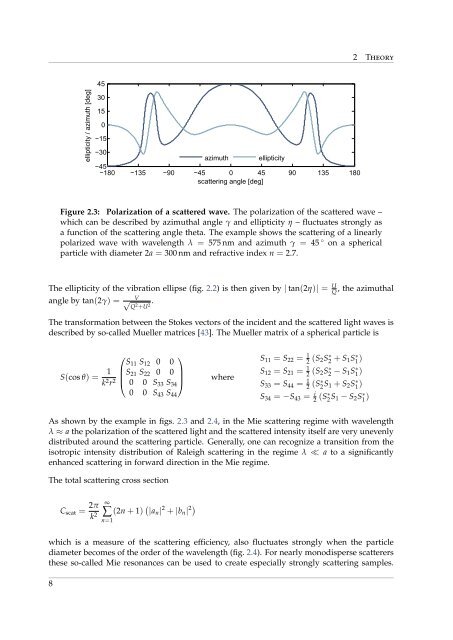
Figure 2.3: Polarization of a scattered wave. The polarization of the scattered wave –
which can be described by azimuthal angle γ and ellipticity η – fluctuates strongly as
a function of the scattering angle theta. The example shows the scattering of a linearly
polarized wave with wavelength λ = 575 nm and azimuth γ = 45 ◦ on a spherical
particle with diameter 2a = 300 nm and refractive index n = 2.7.
The ellipticity of the vibration ellipse (fig. 2.2) is then given by | tan(2η)| = U Q
, the azimuthal
V
angle by tan(2γ) = √Q . 2 +U 2
The transformation between the Stokes vectors of the incident and the scattered light waves is
described by so-called Mueller matrices [43]. The Mueller matrix of a spherical particle is
⎛
⎞
S 11 S 12 0 0
S(cos θ) = 1
⎜S 21 S 22 0 0
⎟
k 2 r 2 ⎝ 0 0 S 33 S 34
⎠
0 0 S 43 S 44
where
S 11 = S 22 = 1 2 (S 2S2 ∗ + S 1S1 ∗)
S 12 = S 21 = 1 2 (S 2S2 ∗ − S 1S1 ∗)
S 33 = S 44 = 1 2 (S∗ 2 S 1 + S 2 S1 ∗)
S 34 = −S 43 = i 2 (S∗ 2 S 1 − S 2 S1 ∗)
As shown by the example in figs. 2.3 and 2.4, in the Mie scattering regime with wavelength
λ ≈ a the polarization of the scattered light and the scattered intensity itself are very unevenly
distributed around the scattering particle. Generally, one can recognize a transition from the
isotropic intensity distribution of Raleigh scattering in the regime λ ≪ a to a significantly
enhanced scattering in forward direction in the Mie regime.
The total scattering cross section
C scat = 2π ∞
k ∑ 2 (2n + 1) ( |a n | 2 + |b n | 2)
n=1
which is a measure of the scattering efficiency, also fluctuates strongly when the particle
diameter becomes of the order of the wavelength (fig. 2.4). For nearly monodisperse scatterers
these so-called Mie resonances can be used to create especially strongly scattering samples.
8