Coherent Backscattering from Multiple Scattering Systems - KOPS ...

More documents

Recommendations

Info

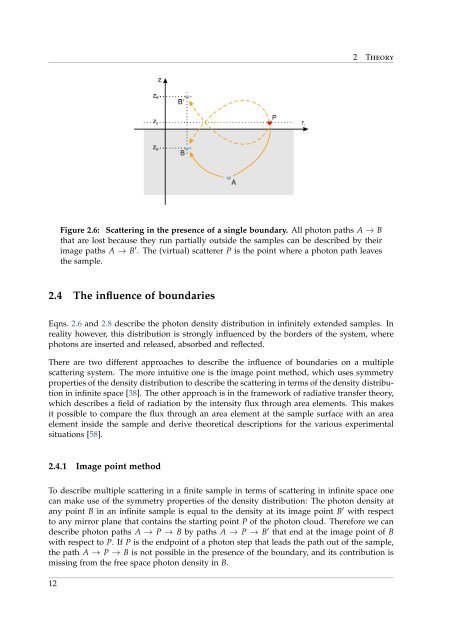
2 Theory Figure 2.6: Scattering in the presence of a single boundary. All photon paths A → B that are lost because they run partially outside the samples can be described by their image paths A → B ′ . The (virtual) scatterer P is the point where a photon path leaves the sample. 2.4 The influence of boundaries Eqns. 2.6 and 2.8 describe the photon density distribution in infinitely extended samples. In reality however, this distribution is strongly influenced by the borders of the system, where photons are inserted and released, absorbed and reflected. There are two different approaches to describe the influence of boundaries on a multiple scattering system. The more intuitive one is the image point method, which uses symmetry properties of the density distribution to describe the scattering in terms of the density distribution in infinite space [38]. The other approach is in the framework of radiative transfer theory, which describes a field of radiation by the intensity flux through area elements. This makes it possible to compare the flux through an area element at the sample surface with an area element inside the sample and derive theoretical descriptions for the various experimental situations [58]. 2.4.1 Image point method To describe multiple scattering in a finite sample in terms of scattering in infinite space one can make use of the symmetry properties of the density distribution: The photon density at any point B in an infinite sample is equal to the density at its image point B ′ with respect to any mirror plane that contains the starting point P of the photon cloud. Therefore we can describe photon paths A → P → B by paths A → P → B ′ that end at the image point of B with respect to P. If P is the endpoint of a photon step that leads the path out of the sample, the path A → P → B is not possible in the presence of the boundary, and its contribution is missing from the free space photon density in B. 12
2.4 The influence of boundaries Figure 2.7: Scattering in the presence of two parallel boundaries. The presence of two parallel boundaries with distance L creates two series of image points B 1 ′ , B′ 2 , B′ 3 , . . . and B 1 ′′, B′′ 2 , . . .. The effective sample thickness L′ = L + 2z 0 simplifies the series. On the other hand, all photon paths that lead to B ′ contain at least one such point P, which is located at an average distance z 0 from the boundary. The photon density that is missing from the free space photon density in B due to the sample boundary is therefore the free space photon density in B ′ , and the photon density distribution in the presence of a boundary becomes ρ(A → B, t) 1 surface = = ρ(A → B, t) − ρ(A → B ′ , t) = e− τ t √ (e ( − ⃗r ⊥,B −⃗r ⊥,A) 2 +(z B −z A ) 2 4Dt − e ( − ⃗r ⊥,B −⃗r ⊥,A) 2 +(−z B +2z 0 −z A ) 2 4Dt 3 4πDt ) (2.9) where we have also considered absorption by its τ-dependent exponential decay. The vector ⃗r ⊥ denotes the components of the position vector⃗r perpendicular to the z-axis and parallel to the sample boundary. Note that z 0 and z B or respectively z A have different signs, as depicted in fig. 2.6. If a second surface opposite to the entrance surface is to be considered, things become a little more complicated. In this case, the photon density in B is the free space photon density distribution minus the photon densities at the two image points B ′ and B ′′ with respect to the two mirror planes in front of the surfaces at z = z 0 and z = L + z 0 . These photon densities again have to be calculated as the densities in the presence of the other surface, and so on. 13
Page 1 and 2: Dissertation Coherent Backscatterin
Page 3 and 4: Ein kurzer Überblick Streuung ist
Page 5 and 6: Ein kurzer Überblick portweglänge
Page 7 and 8: Contents Ein kurzer Überblick i Da
Page 9 and 10: 1 Introduction There have been many
Page 11 and 12: 2 Theory In scattering theory, the
Page 13 and 14: 2.2 Single scattering - Mie theory
Page 15 and 16: 2.2 Single scattering - Mie theory
Page 17 and 18: 2.3 Random walk and diffusion scatt
Page 19: 2.3 Random walk and diffusion of pr
Page 23 and 24: 2.5 Photon flux from a surface The
Page 25 and 26: 2.6 On polarization and interferenc
Page 27 and 28: 2.6 On polarization and interferenc
Page 29 and 30: 2.7 The theory of coherent backscat
Page 31 and 32: 2.7 The theory of coherent backscat
Page 33 and 34: 3 Setups 3.1 Laser System The key p
Page 35 and 36: 3.2 Wide Angle Setup 1 .0 0 .8 h e
Page 37 and 38: 3.3 Small Angle Setup 1 0.998 0.996
Page 39 and 40: 3.3 Small Angle Setup Figure 3.6: T
Page 41 and 42: 3.4 Time Of Flight Setup Figure 3.8
Page 43 and 44: 4 Samples 4.1 Sample characterizati
Page 45 and 46: 4.1 Sample characterization techniq
Page 47 and 48: 4.2 The samples sample particle siz
Page 49 and 50: 4.2 The samples Figure 4.5: Fluidiz
Page 51 and 52: 5 Experiments 5.1 Conservation of e
Page 53 and 54: 5.1 Conservation of energy in coher
Page 65 and 66: 5.2 The coherent backscattering con
Page 71 and 72:
5.2 The coherent backscattering con
Page 73 and 74:
Page 75 and 76:
Page 77 and 78:
6 Summary The focus of the work pre
Page 79 and 80:
Bibliography [1] http://www.schneid
Page 81 and 82:
Bibliography [34] E. Larose, L. Mar
Page 83 and 84:
Figures and Tables Figures Backscat
Page 85 and 86:
Figures and Tables Tables 4.1 Collo
Page 87 and 88:
MATLAB codes Angular intensity dist
Page 89 and 90:
Evaluation of the wide angle data E
Page 91 and 92:
Evaluation of the wide angle data %
Page 93 and 94:
Evaluation of the wide angle data f
Page 95 and 96:
Evaluation of the small angle data
Page 97 and 98:
Page 99:
show all

Coherent Backscattering from Multiple Scattering Systems - KOPS ...

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?