Coherent Backscattering from Multiple Scattering Systems - KOPS ...

2.3 Random walk and diffusion
scattering cross section [m 2 ]
10 −12
10 −14
90 1
120
60
150
0.5
30
180 0
210
330
10 −10 particle radius [m]
10 −7 10 −6
240
270
300
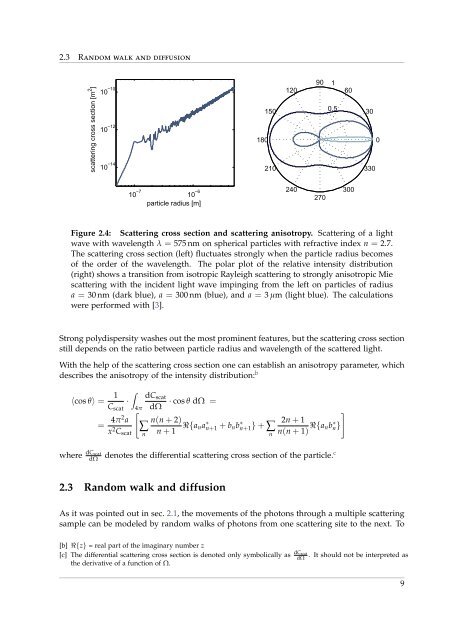
Figure 2.4: Scattering cross section and scattering anisotropy. Scattering of a light
wave with wavelength λ = 575 nm on spherical particles with refractive index n = 2.7.
The scattering cross section (left) fluctuates strongly when the particle radius becomes
of the order of the wavelength. The polar plot of the relative intensity distribution
(right) shows a transition from isotropic Rayleigh scattering to strongly anisotropic Mie
scattering with the incident light wave impinging from the left on particles of radius
a = 30 nm (dark blue), a = 300 nm (blue), and a = 3 µm (light blue). The calculations
were performed with [3].
Strong polydispersity washes out the most prominent features, but the scattering cross section
still depends on the ratio between particle radius and wavelength of the scattered light.
With the help of the scattering cross section one can establish an anisotropy parameter, which
describes the anisotropy of the intensity distribution: b
〈cos θ〉 = 1 ∫
dC scat
· · cos θ dΩ =
C scat 4π dΩ
where dC scat
dΩ
= 4π2 a
x 2 C scat
[∑
n
n(n + 2)
n + 1
R{a na ∗ n+1 + b n bn+1} ∗ + ∑
n
]
2n + 1
n(n + 1) R{a nbn}
∗
denotes the differential scattering cross section of the particle.c
2.3 Random walk and diffusion
As it was pointed out in sec. 2.1, the movements of the photons through a multiple scattering
sample can be modeled by random walks of photons from one scattering site to the next. To
[b] R{z} = real part of the imaginary number z
[c] The differential scattering cross section is denoted only symbolically as dC scat
dΩ . It should not be interpreted as
the derivative of a function of Ω.
9