Coherent Backscattering from Multiple Scattering Systems - KOPS ...

5 Experiments
E sample
(t) / E half−space
(t)
1
0.8
0.6
0.4
0.2
0
free space distribution
half−space distribution
−9.5 −9 −8.5 −8 −7.5 −7 −6.5 −6
log 10
(t [sec])
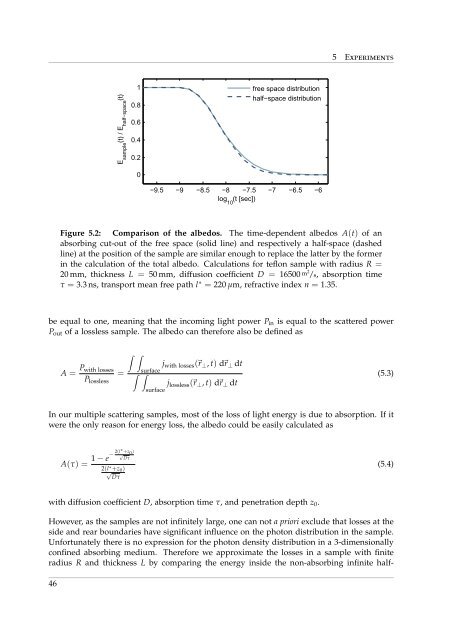
Figure 5.2: Comparison of the albedos. The time-dependent albedos A(t) of an
absorbing cut-out of the free space (solid line) and respectively a half-space (dashed
line) at the position of the sample are similar enough to replace the latter by the former
in the calculation of the total albedo. Calculations for teflon sample with radius R =
20 mm, thickness L = 50 mm, diffusion coefficient D = 16500 m2 /s, absorption time
τ = 3.3 ns, transport mean free path l ∗ = 220 µm, refractive index n = 1.35.
be equal to one, meaning that the incoming light power P in is equal to the scattered power
P out of a lossless sample. The albedo can therefore also be defined as
A = P with losses
P lossless
=
∫ ∫
∫ surface ∫
surface
j with losses (⃗r ⊥ , t) d⃗r ⊥ dt
j lossless (⃗r ⊥ , t) d⃗r ⊥ dt
(5.3)
In our multiple scattering samples, most of the loss of light energy is due to absorption. If it
were the only reason for energy loss, the albedo could be easily calculated as
A(τ) = 1 − 2(l∗ +z 0 )
e− √
Dτ
(5.4)
2(l ∗ +z
√ 0 )
Dτ
with diffusion coefficient D, absorption time τ, and penetration depth z 0 .
However, as the samples are not infinitely large, one can not a priori exclude that losses at the
side and rear boundaries have significant influence on the photon distribution in the sample.
Unfortunately there is no expression for the photon density distribution in a 3-dimensionally
confined absorbing medium. Therefore we approximate the losses in a sample with finite
radius R and thickness L by comparing the energy inside the non-absorbing infinite half-
46