Coherent Backscattering from Multiple Scattering Systems - KOPS ...

4.1 Sample characterization techniques
refractive index
3
2.5
2
1.5
linear
Garnett
1
0 0.2 0.4 0.6 0.8 1
filling fraction
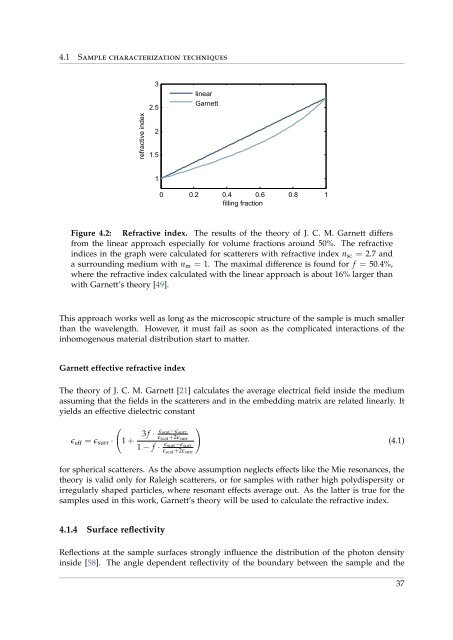
Figure 4.2: Refractive index. The results of the theory of J. C. M. Garnett differs
from the linear approach especially for volume fractions around 50%. The refractive
indices in the graph were calculated for scatterers with refractive index n sc = 2.7 and
a surrounding medium with n m = 1. The maximal difference is found for f = 50.4%,
where the refractive index calculated with the linear approach is about 16% larger than
with Garnett’s theory [49].
This approach works well as long as the microscopic structure of the sample is much smaller
than the wavelength. However, it must fail as soon as the complicated interactions of the
inhomogenous material distribution start to matter.
Garnett effective refractive index
The theory of J. C. M. Garnett [21] calculates the average electrical field inside the medium
assuming that the fields in the scatterers and in the embedding matrix are related linearly. It
yields an effective dielectric constant
ɛ eff = ɛ surr ·
(
1 + 3 f · ɛscat−ɛ )
surr
ɛ scat +2ɛ surr
1 − f · ɛscat−ɛ surr
ɛ scat +2ɛ surr
(4.1)
for spherical scatterers. As the above assumption neglects effects like the Mie resonances, the
theory is valid only for Raleigh scatterers, or for samples with rather high polydispersity or
irregularly shaped particles, where resonant effects average out. As the latter is true for the
samples used in this work, Garnett’s theory will be used to calculate the refractive index.
4.1.4 Surface reflectivity
Reflections at the sample surfaces strongly influence the distribution of the photon density
inside [58]. The angle dependent reflectivity of the boundary between the sample and the
37