Contents Telektronikk - Telenor

14
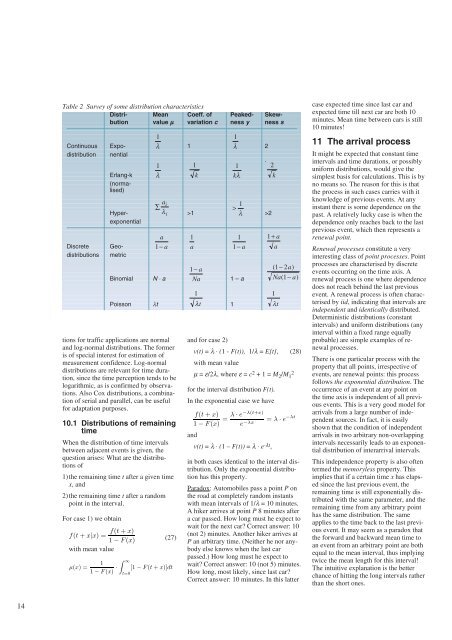
Table 2 Survey of some distribution characteristics
Distri- Mean Coeff. of Peaked- Skewbution
value µµ variation c ness y ness s
1
1
Continuous Expo- λ 1 λ 2
distribution nential
Erlang-k
(normalised)
Discrete Geodistributions
metric
tions for traffic applications are normal
and log-normal distributions. The former
is of special interest for estimation of
measurement confidence. Log-normal
distributions are relevant for time duration,
since the time perception tends to be
logarithmic, as is confirmed by observations.
Also Cox distributions, a combination
of serial and parallel, can be useful
for adaptation purposes.
10.1 Distributions of remaining
time
When the distribution of time intervals
between adjacent events is given, the
question arises: What are the distributions
of
1)the remaining time t after a given time
x, and
2)the remaining time t after a random
point in the interval.
For case 1) we obtain
f(t + x)
f(t + x|x) =
1 − F (x)
with mean value
1
λ
Hyperexponential
>1
>
>2
1
ai ∑
λi λ
a
1− a
Binomial N ⋅ a
1− a
Na 1 – a
Poisson λt λt 1
(27)
1
µ(x) =
1 − F (x) ·
� ∞
[1 − F (t + x)]dt
t=0
1
k
1
a
1
1
kλ
1
1− a
2
k
and for case 2)
v(t) = λ ⋅ (1 - F(t)), 1/λ = E{t}, (28)
with mean value
µ = ε/2λ, where ε = c2 + 1 = M2 /M 2
1
for the interval distribution F(t).
In the exponential case we have
and
v(t) = λ ⋅ (1 – F(t)) = λ ⋅ e-λt ,
1+ a
a
(1− 2a)
Na(1− a)
in both cases identical to the interval distribution.
Only the exponential distribution
has this property.
Paradox: Automobiles pass a point P on
the road at completely random instants
with mean intervals of 1/λ = 10 minutes.
A hiker arrives at point P 8 minutes after
a car passed. How long must he expect to
wait for the next car? Correct answer: 10
(not 2) minutes. Another hiker arrives at
P an arbitrary time. (Neither he nor anybody
else knows when the last car
passed.) How long must he expect to
wait? Correct answer: 10 (not 5) minutes.
How long, most likely, since last car?
Correct answer: 10 minutes. In this latter
1
λt
f(t + x) λ · e−λ(t+x)
=
1 − F (x) e−λx = λ · e −λt
case expected time since last car and
expected time till next car are both 10
minutes. Mean time between cars is still
10 minutes!
11 The arrival process
It might be expected that constant time
intervals and time durations, or possibly
uniform distributions, would give the
simplest basis for calculations. This is by
no means so. The reason for this is that
the process in such cases carries with it
knowledge of previous events. At any
instant there is some dependence on the
past. A relatively lucky case is when the
dependence only reaches back to the last
previous event, which then represents a
renewal point.
Renewal processes constitute a very
interesting class of point processes. Point
processes are characterised by discrete
events occurring on the time axis. A
renewal process is one where dependence
does not reach behind the last previous
event. A renewal process is often characterised
by iid, indicating that intervals are
independent and identically distributed.
Deterministic distributions (constant
intervals) and uniform distributions (any
interval within a fixed range equally
probable) are simple examples of renewal
processes.
There is one particular process with the
property that all points, irrespective of
events, are renewal points: this process
follows the exponential distribution. The
occurrence of an event at any point on
the time axis is independent of all previous
events. This is a very good model for
arrivals from a large number of independent
sources. In fact, it is easily
shown that the condition of independent
arrivals in two arbitrary non-overlapping
intervals necessarily leads to an exponential
distribution of interarrival intervals.
This independence property is also often
termed the memoryless property. This
implies that if a certain time x has elapsed
since the last previous event, the
remaining time is still exponentially distributed
with the same parameter, and the
remaining time from any arbitrary point
has the same distribution. The same
applies to the time back to the last previous
event. It may seem as a paradox that
the forward and backward mean time to
an event from an arbitrary point are both
equal to the mean interval, thus implying
twice the mean length for this interval!
The intuitive explanation is the better
chance of hitting the long intervals rather
than the short ones.