Radiography in Modern Industry - Kodak

More documents

Recommendations

Info

Figure 121: Characteristic curves of a typical industrial x-ray film, developed for 2, 3, 5, 8,and 10 minutes.From the curves shown in Figure 121, values of relative speed and average gradient can bederived as explained earlier. These values, and fog, are plotted against development time inFigure 122. Curves of these quantities plotted against developer temperature, with developmenttime held constant, show a similar form. At the maximum recommended development time of 8minutes, the film used in this example has reached its maximum contrast, and furtherdevelopment would cause a decrease in film contrast, rather than an increase.Figure 122: Time-speed and time-average gradient curves derived from the characteristiccurves of Figure 121. The time-fog curve for the same development conditions is shown.Curves of the type shown in Figure 122 depend on the particular film considered. Some films, forinstance, increase very little in average gradient when the development time is increased from 5to 8 minutes, the main effect being an increase in film speed. A practical point, however, shouldRadiography in Modern Industry 192
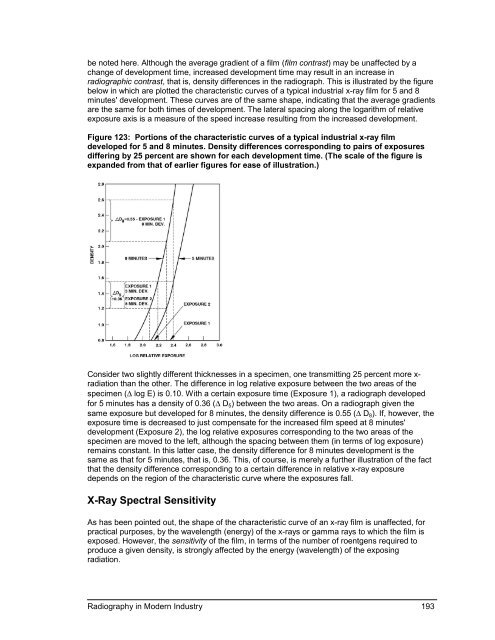
e noted here. Although the average gradient of a film (film contrast) may be unaffected by achange of development time, increased development time may result in an increase inradiographic contrast, that is, density differences in the radiograph. This is illustrated by the figurebelow in which are plotted the characteristic curves of a typical industrial x-ray film for 5 and 8minutes' development. These curves are of the same shape, indicating that the average gradientsare the same for both times of development. The lateral spacing along the logarithm of relativeexposure axis is a measure of the speed increase resulting from the increased development.Figure 123: Portions of the characteristic curves of a typical industrial x-ray filmdeveloped for 5 and 8 minutes. Density differences corresponding to pairs of exposuresdiffering by 25 percent are shown for each development time. (The scale of the figure isexpanded from that of earlier figures for ease of illustration.)Consider two slightly different thicknesses in a specimen, one transmitting 25 percent more x-radiation than the other. The difference in log relative exposure between the two areas of thespecimen (∆ log E) is 0.10. With a certain exposure time (Exposure 1), a radiograph developedfor 5 minutes has a density of 0.36 (∆ D 5 ) between the two areas. On a radiograph given thesame exposure but developed for 8 minutes, the density difference is 0.55 (∆ D 8 ). If, however, theexposure time is decreased to just compensate for the increased film speed at 8 minutes'development (Exposure 2), the log relative exposures corresponding to the two areas of thespecimen are moved to the left, although the spacing between them (in terms of log exposure)remains constant. In this latter case, the density difference for 8 minutes development is thesame as that for 5 minutes, that is, 0.36. This, of course, is merely a further illustration of the factthat the density difference corresponding to a certain difference in relative x-ray exposuredepends on the region of the characteristic curve where the exposures fall.X-Ray Spectral SensitivityAs has been pointed out, the shape of the characteristic curve of an x-ray film is unaffected, forpractical purposes, by the wavelength (energy) of the x-rays or gamma rays to which the film isexposed. However, the sensitivity of the film, in terms of the number of roentgens required toproduce a given density, is strongly affected by the energy (wavelength) of the exposingradiation.Radiography in Modern Industry 193
Page 1 and 2:
RadiographyinModernIndustry
Page 3 and 4:
RadiographyinModernIndustryFOURTH E
Page 5 and 6:
ContentsIntroduction...............
Page 7 and 8:
Chapter 1: The Radiographic Process
Page 9 and 10:
Intensifying ScreensX-ray and other
Page 11 and 12:
makes it a very suitable material f
Page 13 and 14:
Figure 6: Typical voltage waveforms
Page 15 and 16:
Table I - Typical X-ray Machines an
Page 17 and 18:
The wavelengths (or energies of rad
Page 19 and 20:
Table III - Industrial Gamma-Ray So
Page 21 and 22:
1. The source of light should be sm
Page 23 and 24:
B and H in the Figure 13 show the e
Page 25 and 26:
Figure 14: Geometric construction f
Page 27 and 28:
Figure 17: Pinhole pictures of the
Page 29 and 30:
The kilovoltage applied to the x-ra
Page 31 and 32:
Figure 21: Schematic diagram of som
Page 33 and 34:
kind of material radiographed, the
Page 35 and 36:
instance, the kilovoltage may be fi
Page 37 and 38:
The technique need not be limited t
Page 39 and 40:
Chapter 5: Radiographic ScreensWhen
Page 41 and 42:
Contact between the film and the le
Page 43 and 44:
Figure 29: The number of electrons
Page 45 and 46:
lead foil screens ran be retained w
Page 47 and 48:
Figure 33: The sharpness of the rad
Page 49 and 50:
Figure 34: Low density (right) is a
Page 51 and 52:
such as a wall or floor, on the fil
Page 53 and 54:
from this source. Since scatter als
Page 55 and 56:
A filter reduces excessive subject
Page 57 and 58:
Definite rules as to filter thickne
Page 59 and 60:
0.010-inch front screen of value be
Page 61 and 62:
Example: Suppose that with a given
Page 63 and 64:
If the milliamperage remains consta
Page 65 and 66:
espectively. In other words, a cons
Page 67 and 68:
Any given exposure chart applies to
Page 69 and 70:
Figure 46: Typical gamma-ray exposu
Page 71 and 72:
where the slope of the characterist
Page 73 and 74:
Figure 49: Characteristic curves of
Page 75 and 76:
Figure 51: Characteristic curve of
Page 77 and 78:
Nomogram MethodsIn Figure 54, the s
Page 79 and 80:
Figure 56: Transparent overlay posi
Page 81 and 82:
Figure 58: Overlay positioned so as
Page 83 and 84:
The problem of radiographing a part
Page 85 and 86:
Figure 62: System of lines drawn on
Page 87 and 88:
Chapter 8: Radiographic Image Quali
Page 89 and 90:
Film contrast refers to the slope (
Page 91 and 92:
Hole Type PenetrametersThe common p
Page 93 and 94:
of the same thickness as the specim
Page 95 and 96:
Chapter 9: Industrial X-ray FilmsMo
Page 97 and 98:
Figure 70 indicates the direction t
Page 99 and 100:
the lead letters on a radiation-abs
Page 101 and 102:
Therefore, protection requirements
Page 103 and 104:
5. Avoid pressure damage caused by
Page 105 and 106:
Paddles or plunger-type agitators a
Page 107 and 108:
slow, and the development time reco
Page 109 and 110:
ubbles make their way to the surfac
Page 111 and 112:
When development is complete, the f
Page 113 and 114:
soften considerably with prolonged
Page 115 and 116:
Figure 77: The roller transport sys
Page 117 and 118:
Rapid Access to Processed Radiograp
Page 119 and 120:
Figure 78: Film-feeding procedures
Page 121 and 122:
Chapter 11: Process ControlUsers of
Page 123 and 124:
3. Age of the developer replenisher
Page 125 and 126:
Figure 80: Control chart below for
Page 127 and 128:
DiscussionDensitometric data and pr
Page 129 and 130:
Figure 82: Plan of a manual x-ray p
Page 131 and 132:
Figure 83: A schematic diagram of a
Page 133 and 134:
loading-bench activities are carrie
Page 135 and 136:
KODAK Quinone-Thiosulfate Intensifi
Page 137 and 138:
Methylene-Blue MethodTwo variations
Page 139 and 140:
KODAK Hypo Test Solution HT-2Avoird
Page 141 and 142: In summary, use of the test papers
Page 143 and 144: narrow angle would be very thick, e
Page 145 and 146: When radiation passes through a spe
Page 147 and 148: Figure 89: Demonstration of the eff
Page 149 and 150: Figure 90: The amount of gamma radi
Page 151 and 152: The radiograph exposed in the right
Page 153 and 154: To illustrate, let us assume that t
Page 155 and 156: Figure 95: High-speed x-ray picture
Page 157 and 158: Figure 97: Two methods of neutron r
Page 159 and 160: Duplicating RadiographsSimultaneous
Page 161 and 162: Sometimes, as when sets of referenc
Page 163 and 164: PhotofluorographyIn photofluorograp
Page 165 and 166: discontinuities or of segregation i
Page 167 and 168: from the camera or by reaching down
Page 169 and 170: Figure 106: Schematic diagram of th
Page 171 and 172: valuable technique, for instance, i
Page 173 and 174: The position of the spots is determ
Page 175 and 176: Powder Diffraction File, Internatio
Page 177 and 178: Processing TechniquesRadiographs on
Page 179 and 180: Since this formula applies only to
Page 181 and 182: such that it does not distort the i
Page 183 and 184: Figure 113: A: Representation of a
Page 185 and 186: Figure 115: Characteristic curve of
Page 187 and 188: film fairly well. If high densities
Page 189 and 190: Density = 1.5 Density = 2.5Film Rel
Page 191: In most industrial radiography, the
Page 195 and 196: Chapter 17: Film Graininess; Signal
Page 197 and 198: The ratio of signal to noise has a
Page 199 and 200: Chapter 18: The Photographic Latent
Page 201 and 202: Thus, the change that makes an expo
Page 203 and 204: Figure 130: Stages in the developme
Page 205 and 206: electrons by successive Compton int
Page 207 and 208: Development is essentially a chemic
Page 209 and 210: Chapter 19: ProtectionOne of the mo
Page 211 and 212: duct is brought into the x-ray room
show all

Radiography in Modern Industry - Kodak

Create successful ePaper yourself

Delete template?

Save as template?