Reviews in Computational Chemistry Volume 18
Reviews in Computational Chemistry Volume 18
Reviews in Computational Chemistry Volume 18
- No tags were found...
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>18</strong>0 Charge-Transfer Reactions <strong>in</strong> Condensed Phases<br />
In many practical cases, the factors fei are very close to unity and can be<br />
omitted. The parameters ~a0i and ~m0i are then equal to their gas-phase values<br />
a0i and m0i. Equation [100] then gives the polarizability change <strong>in</strong> terms of<br />
spectroscopic moments and gas-phase solute dipoles. Experimental measurement<br />
and theoretical calculation of a0 ¼ a02 a01 is still challeng<strong>in</strong>g.<br />
Perhaps the most accurate way to measure a0 presently available is that<br />
by Stark spectroscopy, 74–76 which also gives m0. Equation [100] can therefore<br />
be used as an <strong>in</strong>dependent source of a0, provided all other parameters<br />
are available, or as a consistency test for the band shape analysis.<br />
One of the consequences of a nonzero a0 is that the relation between<br />
the solvent-<strong>in</strong>duced Stokes shift and the correspond<strong>in</strong>g spectral width (lv ¼ 0)<br />
h nst ¼ bs 2<br />
½101Š<br />
which is valid for l<strong>in</strong>ear solvation response and a0 ¼ 0, does not hold any<br />
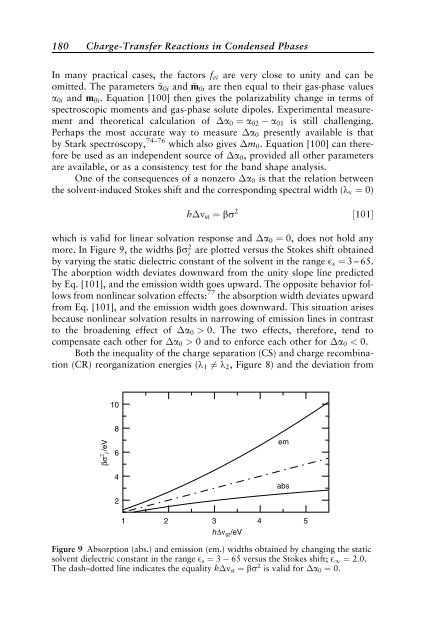
more. In Figure 9, the widths bs2 i are plotted versus the Stokes shift obta<strong>in</strong>ed<br />
by vary<strong>in</strong>g the static dielectric constant of the solvent <strong>in</strong> the range Es ¼ 3 – 65.<br />
The aborption width deviates downward from the unity slope l<strong>in</strong>e predicted<br />
by Eq. [101], and the emission width goes upward. The opposite behavior follows<br />
from nonl<strong>in</strong>ear solvation effects: 77 the absorption width deviates upward<br />
from Eq. [101], and the emission width goes downward. This situation arises<br />
because nonl<strong>in</strong>ear solvation results <strong>in</strong> narrow<strong>in</strong>g of emission l<strong>in</strong>es <strong>in</strong> contrast<br />
to the broaden<strong>in</strong>g effect of a0 > 0. The two effects, therefore, tend to<br />
compensate each other for a0 > 0 and to enforce each other for a0 < 0.<br />
Both the <strong>in</strong>equality of the charge separation (CS) and charge recomb<strong>in</strong>ation<br />
(CR) reorganization energies (l1 6¼ l2, Figure 8) and the deviation from<br />
βσ 2 i /eV<br />
10<br />
8<br />
6<br />
4<br />
2<br />
em<br />
abs<br />
1 2 3 4 5<br />
h ∆ν st /eV<br />
Figure 9 Absorption (abs.) and emission (em.) widths obta<strong>in</strong>ed by chang<strong>in</strong>g the static<br />
solvent dielectric constant <strong>in</strong> the range Es ¼ 3 65 versus the Stokes shift; E1 ¼ 2:0.<br />
The dash–dotted l<strong>in</strong>e <strong>in</strong>dicates the equality h nst ¼ bs 2 is valid for a0 ¼ 0.