Reviews in Computational Chemistry Volume 18

it by choosing the GMH basis set 7 ). In this case, the CT free energy surface is
defined by Eq. [41] with the following energy gap:
E d ðY d Þ¼½ E 2 12 þ 2 I abð F d s Y d Þþð F d s Y d Þ 2 Š 1=2
½119Š
The diabatic and adiabatic formulations can be compared when the condition
Eab ¼ 0 is imposed. Then, one obtains Yad ¼ eYd , l I ¼ l d , FI s ¼ Fd s .
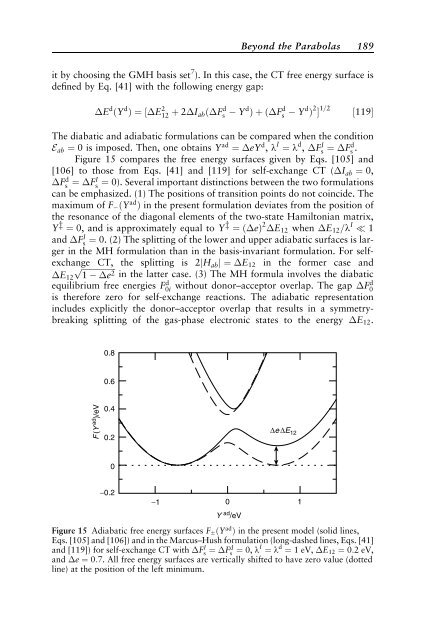
Figure 15 compares the free energy surfaces given by Eqs. [105] and
[106] to those from Eqs. [41] and [119] for self-exchange CT ( Iab ¼ 0,
Fd s ¼ FI s ¼ 0). Several important distinctions between the two formulations
can be emphasized. (1) The positions of transition points do not coincide. The
maximum of F ðYadÞ in the present formulation deviates from the position of
the resonance of the diagonal elements of the two-state Hamiltonian matrix,
Yz ¼ 0, and is approximately equal to Yz ¼ð eÞ 2 E12 when E12=l I
1
and FI s ¼ 0. (2) The splitting of the lower and upper adiabatic surfaces is larger
in the MH formulation than in the basis-invariant formulation. For selfexchange
CT, the splitting is 2jHabj ¼ E12 ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
in the former case and
1 e2 p
in the latter case. (3) The MH formula involves the diabatic
E12
equilibrium free energies Fd 0i without donor–acceptor overlap. The gap Fd 0
is therefore zero for self-exchange reactions. The adiabatic representation
includes explicitly the donor–acceptor overlap that results in a symmetrybreaking
splitting of the gas-phase electronic states to the energy E12.
F (Y ad )/eV
0.8
0.6
0.4
0.2
0
−0.2
∆e ∆E 12
−1 0
Y
1
ad /eV
Beyond the Parabolas 189
Figure 15 Adiabatic free energy surfaces F ðY ad Þ in the present model (solid lines,
Eqs. [105] and [106]) and in the Marcus–Hush formulation (long-dashed lines, Eqs. [41]
and [119]) for self-exchange CT with F I s ¼ Fd s ¼ 0, lI ¼ l d ¼ 1 eV, E12 ¼ 0:2 eV,
and e ¼ 0:7. All free energy surfaces are vertically shifted to have zero value (dotted
line) at the position of the left minimum.