Leonhard EULER

14
1. MILNÍKY MATEMATIKY PŘED EULEREM
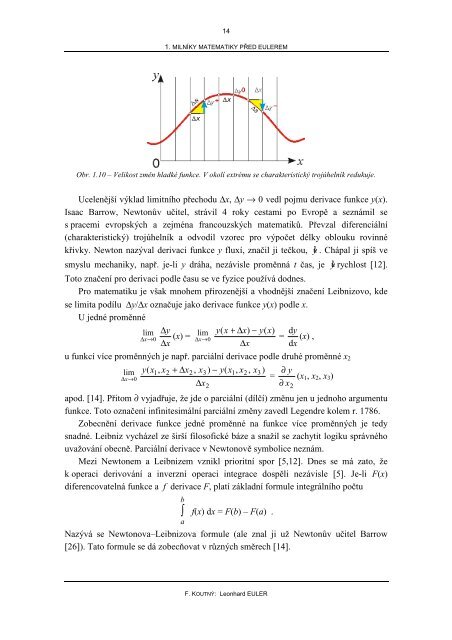
Obr. 1.10 – Velikost změn hladké funkce. V okolí extrému se charakteristický trojúhelník redukuje.
Ucelenější výklad limitního přechodu ∆x, ∆y → 0 vedl pojmu derivace funkce y(x).
Isaac Barrow, Newtonův učitel, strávil 4 roky cestami po Evropě a seznámil se
s pracemi evropských a zejména francouzských matematiků. Převzal diferenciální
(charakteristický) trojúhelník a odvodil vzorec pro výpočet délky oblouku rovinné
křivky. Newton nazýval derivaci funkce y fluxí, značil ji tečkou, y& . Chápal ji spíš ve
smyslu mechaniky, např. je-li y dráha, nezávisle proměnná t čas, je y& rychlost [12].
Toto značení pro derivaci podle času se ve fyzice používá dodnes.
Pro matematiku je však mnohem přirozenější a vhodnější značení Leibnizovo, kde
se limita podílu ∆y/∆x označuje jako derivace funkce y(x) podle x.
U jedné proměnné
lim
→0 ∆x
∆ y (x) =
lim
∆x→
0
∆x
y(
x + ∆x)
− y(
x)
=
∆x
d y (x) ,
dx
u funkcí více proměnných je např. parciální derivace podle druhé proměnné x 2
lim y(
x1 , x2
+ ∆x2
, x3)
− y(
x1,
x2
, x3)
∂ y
→0
= (x 1 , x 2 , x 3 )
∆x
∂
∆x
2
apod. [14]. Přitom ∂ vyjadřuje, že jde o parciální (dílčí) změnu jen u jednoho argumentu
funkce. Toto označení infinitesimální parciální změny zavedl Legendre kolem r. 1786.
Zobecnění derivace funkce jedné proměnné na funkce více proměnných je tedy
snadné. Leibniz vycházel ze širší filosofické báze a snažil se zachytit logiku správného
uvažování obecně. Parciální derivace v Newtonově symbolice neznám.
Mezi Newtonem a Leibnizem vznikl prioritní spor [5,12]. Dnes se má zato, že
k operaci derivování a inverzní operaci integrace dospěli nezávisle [5]. Je-li F(x)
diferencovatelná funkce a f derivace F, platí základní formule integrálního počtu
b
∫ f(x) dx = F(b) – F(a) .
a
Nazývá se Newtonova–Leibnizova formule (ale znal ji už Newtonův učitel Barrow
[26]). Tato formule se dá zobecňovat v různých směrech [14].
x 2
F. KOUTNÝ: Leonhard EULER