Leonhard EULER

41
3. EULEROVY MATEMATICKÉ PRÁCE
Funkci, kterou jsme označili podle Riemanna ζ(s) [68], vyšetřoval pro s > 1 už
Euler. Roku 1735 ve věku 28 let rozřešil tzv. basilejský problém [69]: čemu se rovná
∑ ∞ =1 k
1
2
k
? Nikomu před ním, ani Bernoulliům, se nepodařilo najít odpověď. Eulerův
postup je podrobně vyložen v práci [70].
n S n (2)
10 1 1.5497677317
10 2 1.6349839002
10 3 1.6439345667
10 4 1.6448340718
10 5 1.6449240669
10 6 1.6449330668
10 7 1.6449339668
10 8 1.6449340568
10 9 1.6449340658
10 10 1.6449340666
a obecně pro sudá čísla ζ(2n) =
Součty sudých mocnin k
1
se dnes zmiňují v teorii funkcí
komplexní proměnné jako příklad aplikace rozvoje funkce
cot z = cos z/sin z v Taylorovu (či Laurentovu) řadu a reziduové
věty [71, 72,14]. Euler však byl mistr manipulací s řadami a
delším postupem [70] dospěl k výsledku, že
ζ(2) = ∑ ∞
k=1
Později ukázal, že
ζ(4) = ∑ ∞
k=1
2n
B2
n π
2
(2n)!
1
2
k
1
4
k
=
2
π =1.644 934 066 848…
6
4
= π = 1.082 323 233 711…
90
, kde B 2n jsou Bernoulliho čísla (= koeficienty
z z
rozvoje
e z = 1 – +
−1 2 ∑ ∞ B
n
2 k
z 2k ). Dále platí
(2k)!
∑ ⎜
⎛ n + 1
⎟
⎞ Bk = 0 [72], což po zadání B
k=1
k=
0 ⎝ k
0 = 1
⎠
umožňuje snadné rekurentní počítání B k na počítači. Tabulka B k je na str. 51. Další informace a seznam
B 2k ve tvaru zlomků (podílů celých čísel) pro k =1, …, 20 jsou v [73]).
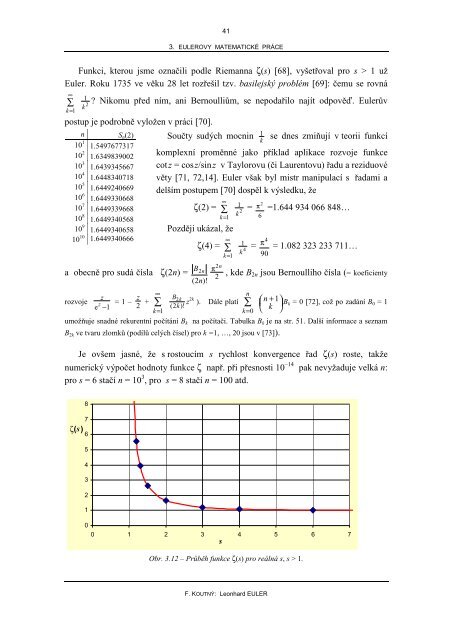
Je ovšem jasné, že s rostoucím s rychlost konvergence řad ζ(s) roste, takže
numerický výpočet hodnoty funkce ζ např. při přesnosti 10 –14 pak nevyžaduje velká n:
pro s = 6 stačí n = 10 3 , pro s = 8 stačí n = 100 atd.
z(s)
8
7
6
5
4
3
2
1
0
0 1 2 3 4 5 6 7
s
Obr. 3.12 – Průběh funkce ζ(s) pro reálná s, s > 1.
F. KOUTNÝ: Leonhard EULER