Hinweise zum Praktikum und zur Auswertung von Messergebnissen
Hinweise zum Praktikum und zur Auswertung von Messergebnissen
Hinweise zum Praktikum und zur Auswertung von Messergebnissen
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
78 rückmann, glüge <strong>und</strong> windzio<br />
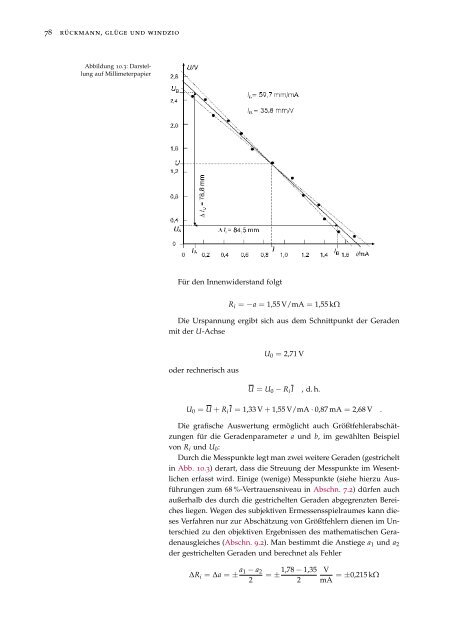
Abbildung 10.3: Darstellung<br />
auf Millimeterpapier<br />
Für den Innenwiderstand folgt<br />
R i = −a = 1,55 V/mA = 1,55 kΩ<br />
Die Urspannung ergibt sich aus dem Schnittpunkt der Geraden<br />
mit der U-Achse<br />
oder rechnerisch aus<br />
U0 = 2,71 V<br />
U = U0 − R i I , d. h.<br />
U0 = U + R i I = 1,33 V + 1,55 V/mA · 0,87 mA = 2,68 V .<br />
Die grafische <strong>Auswertung</strong> ermöglicht auch Größtfehlerabschätzungen<br />
für die Geradenparameter a <strong>und</strong> b, im gewählten Beispiel<br />
<strong>von</strong> R i <strong>und</strong> U0:<br />
Durch die Messpunkte legt man zwei weitere Geraden (gestrichelt<br />
in Abb. 10.3) derart, dass die Streuung der Messpunkte im Wesentlichen<br />
erfasst wird. Einige (wenige) Messpunkte (siehe hierzu Ausführungen<br />
<strong>zum</strong> 68 %-Vertrauensniveau in Abschn. 7.2) dürfen auch<br />
außerhalb des durch die gestrichelten Geraden abgegrenzten Bereiches<br />
liegen. Wegen des subjektiven Ermessensspielraumes kann dieses<br />
Verfahren nur <strong>zur</strong> Abschätzung <strong>von</strong> Größtfehlern dienen im Unterschied<br />
zu den objektiven Ergebnissen des mathematischen Geradenausgleiches<br />
(Abschn. 9.2). Man bestimmt die Anstiege a1 <strong>und</strong> a2<br />
der gestrichelten Geraden <strong>und</strong> berechnet als Fehler<br />
∆R i = ∆a = ± a1 − a2<br />
2<br />
1,78 − 1,35<br />
= ±<br />
2<br />
V<br />
= ±0,215 kΩ<br />
mA