a la physique de l'information - Lisa - Université d'Angers

exposant τ(q)
15
10
5
0
−5
−10
−15
−20
−25
−30
−35
−40
−45
−5 −4 −3 −2 −1 0 1 2 3 4 5
exposant q
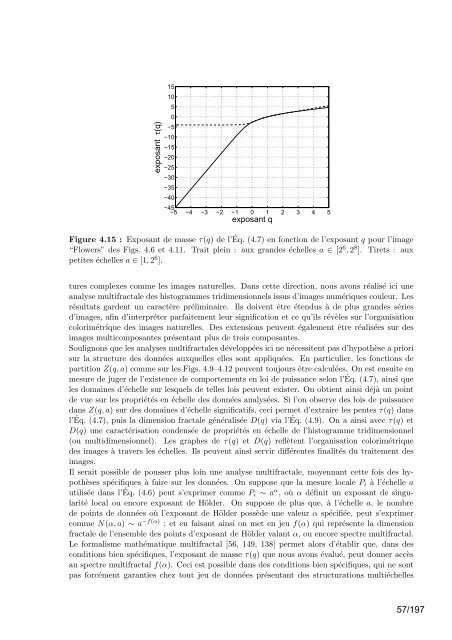
Figure 4.15 : Exposant de masse τ(q) de l’ Éq. (4.7) en fonction de l’exposant q pour l’image
“Flowers” des Figs. 4.6 et 4.11. Trait plein : aux grandes échelles a ∈ [26 , 28 ]. Tirets : aux
petites échelles a ∈ [1, 26 ].
tures complexes comme les images naturelles. Dans cette direction, nous avons réalisé ici une
analyse multifractale des histogrammes tridimensionnels issus d’images numériques couleur. Les
résultats gardent un caractère préliminaire. Ils doivent être étendus à de plus grandes séries
d’images, afin d’interpréter parfaitement leur signification et ce qu’ils révèles sur l’organisation
colorimétrique des images naturelles. Des extensions peuvent également être réalisées sur des
images multicomposantes présentant plus de trois composantes.
Soulignons que les analyses multifractales développées ici ne nécessitent pas d’hypothèse a priori
sur la structure des données auxquelles elles sont appliquées. En particulier, les fonctions de
partition Z(q, a) comme sur les Figs. 4.9–4.12 peuvent toujours être calculées. On est ensuite en
mesure de juger de l’existence de comportements en loi de puissance selon l’ Éq. (4.7), ainsi que
les domaines d’échelle sur lesquels de telles lois peuvent exister. On obtient ainsi déjà un point
de vue sur les propriétés en échelle des données analysées. Si l’on observe des lois de puissance
dans Z(q, a) sur des domaines d’échelle significatifs, ceci permet d’extraire les pentes τ(q) dans
l’ Éq. (4.7), puis la dimension fractale généralisée D(q) via l’Éq. (4.9). On a ainsi avec τ(q) et
D(q) une caractérisation condensée de propriétés en échelle de l’histogramme tridimensionnel
(ou multidimensionnel). Les graphes de τ(q) et D(q) reflètent l’organisation colorimétrique
des images à travers les échelles. Ils peuvent ainsi servir différentes finalités du traitement des
images.
Il serait possible de pousser plus loin une analyse multifractale, moyennant cette fois des hypothèses
spécifiques à faire sur les données. On suppose que la mesure locale Pi à l’échelle a
utilisée dans l’ Éq. (4.6) peut s’exprimer comme Pi ∼ a α , où α définit un exposant de singularité
local ou encore exposant de Hölder. On suppose de plus que, à l’échelle a, le nombre
de points de données où l’exposant de Hölder possède une valeur α spécifiée, peut s’exprimer
comme N(α, a) ∼ a −f(α) ; et en faisant ainsi on met en jeu f(α) qui représente la dimension
fractale de l’ensemble des points d’exposant de Hölder valant α, ou encore spectre multifractal.
Le formalisme mathématique multifractal [56, 149, 138] permet alors d’établir que, dans des
conditions bien spécifiques, l’exposant de masse τ(q) que nous avons évalué, peut donner accès
au spectre multifractal f(α). Ceci est possible dans des conditions bien spécifiques, qui ne sont
pas forcément garanties chez tout jeu de données présentant des structurations multiéchelles
57/197