software to fit optical spectra - Quantum Materials Group

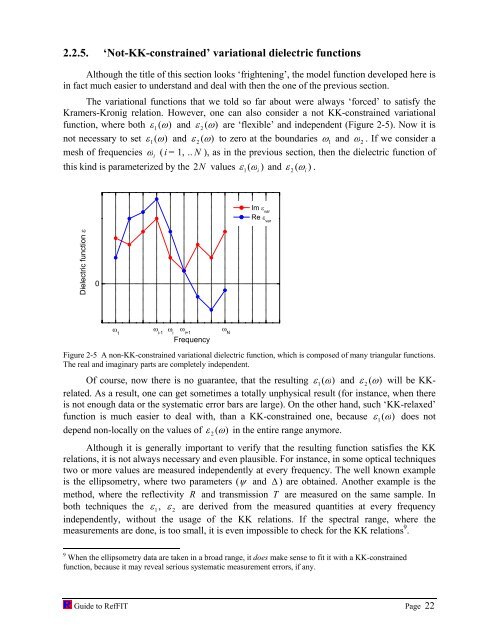
2.2.5. ‘Not-KK-constrained’ variational dielectric functions
Although the title of this section looks ‘frightening’, the model function developed here is
in fact much easier to understand and deal with then the one of the previous section.
The variational functions that we told so far about were always ‘forced’ to satisfy the
Kramers-Kronig relation. However, one can also consider a not KK-constrained variational
function, where both ε 1( ω)
and ε 2 ( ω)
are ‘flexible’ and independent (Figure 2-5). Now it is
not necessary to set ε 1( ω)
and ε 2 ( ω)
to zero at the boundaries ω 1 and ω 2 . If we consider a
mesh of frequencies ω i (i = 1, .. N ), as in the previous section, then the dielectric function of
this kind is parameterized by the 2 N values ε ( ω ) and ε ( ω ) .
Dielectric function ε
0
ω 1
ω i-1
ω i
ω i+1
Frequency
ω N
1 i
Im ε var
Re ε var
Figure 2-5 A non-KK-constrained variational dielectric function, which is composed of many triangular functions.
The real and imaginary parts are completely independent.
Of course, now there is no guarantee, that the resulting ε 1( ω)
and ε 2 ( ω)
will be KKrelated.
As a result, one can get sometimes a totally unphysical result (for instance, when there
is not enough data or the systematic error bars are large). On the other hand, such ‘KK-relaxed’
function is much easier to deal with, than a KK-constrained one, because ε 1( ω)
does not
depend non-locally on the values of ε ( ) in the entire range anymore.
2 ω
Although it is generally important to verify that the resulting function satisfies the KK
relations, it is not always necessary and even plausible. For instance, in some optical techniques
two or more values are measured independently at every frequency. The well known example
is the ellipsometry, where two parameters (ψ and ∆ ) are obtained. Another example is the
method, where the reflectivity R and transmission T are measured on the same sample. In
both techniques the ε 1,
ε 2 are derived from the measured quantities at every frequency
independently, without the usage of the KK relations. If the spectral range, where the
measurements are done, is too small, it is even impossible to check for the KK relations 9 .
9 When the ellipsometry data are taken in a broad range, it does make sense to fit it with a KK-constrained
function, because it may reveal serious systematic measurement errors, if any.
Guide to RefFIT Page 22
2 i