The Development of Neural Network Based System Identification ...

More documents

Recommendations

Info

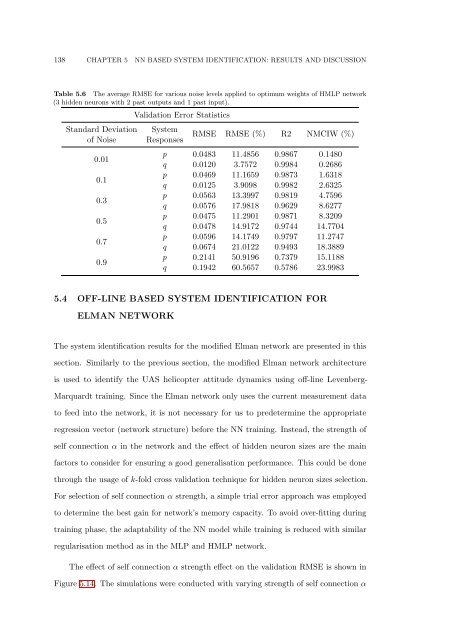
138 CHAPTER 5 NN BASED SYSTEM IDENTIFICATION: RESULTS AND DISCUSSION Table 5.6 The average RMSE for various noise levels applied to optimum weights of HMLP network (3 hidden neurons with 2 past outputs and 1 past input). Standard Deviation of Noise 0.01 0.1 0.3 0.5 0.7 0.9 Validation Error Statistics System Responses RMSE RMSE (%) R2 NMCIW (%) p 0.0483 11.4856 0.9867 0.1480 q 0.0120 3.7572 0.9984 0.2686 p 0.0469 11.1659 0.9873 1.6318 q 0.0125 3.9098 0.9982 2.6325 p 0.0563 13.3997 0.9819 4.7596 q 0.0576 17.9818 0.9629 8.6277 p 0.0475 11.2901 0.9871 8.3209 q 0.0478 14.9172 0.9744 14.7704 p 0.0596 14.1749 0.9797 11.2747 q 0.0674 21.0122 0.9493 18.3889 p 0.2141 50.9196 0.7379 15.1188 q 0.1942 60.5657 0.5786 23.9983 5.4 OFF-LINE BASED SYSTEM IDENTIFICATION FOR ELMAN NETWORK The system identification results for the modified Elman network are presented in this section. Similarly to the previous section, the modified Elman network architecture is used to identify the UAS helicopter attitude dynamics using off-line Levenberg- Marquardt training. Since the Elman network only uses the current measurement data to feed into the network, it is not necessary for us to predetermine the appropriate regression vector (network structure) before the NN training. Instead, the strength of self connection α in the network and the effect of hidden neuron sizes are the main factors to consider for ensuring a good generalisation performance. This could be done through the usage of k-fold cross validation technique for hidden neuron sizes selection. For selection of self connection α strength, a simple trial error approach was employed to determine the best gain for network’s memory capacity. To avoid over-fitting during training phase, the adaptability of the NN model while training is reduced with similar regularisation method as in the MLP and HMLP network. The effect of self connection α strength effect on the validation RMSE is shown in Figure 5.14. The simulations were conducted with varying strength of self connection α
5.4 OFF-LINE BASED SYSTEM IDENTIFICATION FOR ELMAN NETWORK 139 10 3 Self Connection Strengh, α 10 2 RMSE (%) 10 1 10 0 −0.2 0 0.2 0.4 0.6 0.8 1 1.2 Figure 5.14 The self connection α strength selection results using modified Elman network with reduced connection. The Elman network training are repeated 10 times and validated on a test set. The training is carried out using 6 hidden neurons. from 0 to 1 to investigate the prediction performance of basic Elman network (α = 0) and modified Elman network. Finding from the plot shows that the self connection values between 0.3 to 0.5 produced satisfactory prediction performance before RMSE values increase beyond α = 0.6. The lowest RMSE value is found at α = 0.5 with 14.24 ± 1.26% and this is used throughout the analysis. The result of neurons size selection is reproduced here for the modified Elman network using the k-fold cross validation method. The result of the hidden neurons selection for 1 past output and 1 past input (4 regressors) network structure is given in Figure 5.15. From the plot, the network structure with 1 past input and 1 past output measurement produces an acceptable RMSE percentage between hidden neuron sizes h = 4 → 10, thus it is logical to select the optimum neuron size at h = 4. Finally, we arrive at the following network specifications (Table 5.7) that adequately represent the attitude dynamics of a model scaled helicopter. Note that the total number of weights in the optimum Elman network is lesser than the optimum MLP and HMLP network. The corresponding one-step ahead prediction of the angular rate responses that are
Page 1:
The Development of Neural Network B
Page 5 and 6:
ABSTRACT This thesis presents the d
Page 7:
vii the MLP network, the prediction
Page 11:
PUBLICATIONS The following is a lis
Page 14 and 15:
xiv TABLE OF CONTENTS CHAPTER 4 CHA
Page 17 and 18:
LIST OF FIGURES 1.1 Examples of typ
Page 19 and 20:
LIST OF FIGURES xix 3.13 Overview o
Page 21 and 22:
LIST OF FIGURES xxi 5.2 The predict
Page 23 and 24:
LIST OF FIGURES xxiii 5.13 The pred
Page 25 and 26:
LIST OF FIGURES xxv 7.1 The locatio
Page 27 and 28:
LIST OF TABLES 3.1 The specificatio
Page 29 and 30:
NOMENCLATURE AFCS Automatic Flight
Page 31:
LIST OF TABLES xxxi NNARX QP RBF RC
Page 34 and 35:
2 CHAPTER 1 INTRODUCTION Surveillan
Page 36 and 37:
4 CHAPTER 1 INTRODUCTION is then de
Page 38 and 39:
6 CHAPTER 1 INTRODUCTION the dynami
Page 40 and 41:
8 CHAPTER 1 INTRODUCTION models [Sa
Page 42 and 43:
10 CHAPTER 1 INTRODUCTION improved
Page 44 and 45:
12 CHAPTER 1 INTRODUCTION Chapter 3
Page 47 and 48:
Chapter 2 LITERATURE REVIEW The pur
Page 49 and 50:
2.1 INTRODUCTION 17 • Inefficient
Page 51 and 52:
2.1 INTRODUCTION 19 Figure 2.2 The
Page 53 and 54:
2.2 HELICOPTER DYNAMICS MODELLING A
Page 55 and 56:
Page 57 and 58:
Page 59 and 60:
2.3 NEURAL NETWORK BASED SYSTEM IDE
Page 61 and 62:
Page 63 and 64:
Page 65 and 66:
Page 67 and 68:
Page 69 and 70:
2.4 AUTOMATIC FLIGHT CONTROL SYSTEM
Page 71 and 72:
Page 73 and 74:
Page 75 and 76:
Page 77 and 78:
Page 79 and 80:
Page 81 and 82:
Page 83 and 84:
Page 85:
2.5 SUMMARY 53 design based on the
Page 88 and 89:
56 CHAPTER 3 AERIAL PLATFORM AND CU
Page 90 and 91:
Page 92 and 93:
Page 94 and 95:
Page 96 and 97:
Page 98 and 99:
Page 100 and 101:
Page 102 and 103:
Page 104 and 105:
Page 106 and 107:
Page 109 and 110:
Chapter 4 NEURAL NETWORK BASED SYST
Page 111 and 112:
4.2 THE ARTIFICIAL NEURAL NETWORKS
Page 113 and 114:
Page 115 and 116:
Page 117 and 118:
Page 119 and 120: 4.2 THE ARTIFICIAL NEURAL NETWORKS
Page 121 and 122: 4.2 THE ARTIFICIAL NEURAL NETWORKS
Page 123 and 124: 4.3 SYSTEM IDENTIFICATION WITH NEUR
Page 149 and 150: 4.4 SUMMARY 117 Segment 1 Segment 2
Page 151 and 152: Chapter 5 NN BASED SYSTEM IDENTIFIC
Page 153 and 154: 5.2 OFF-LINE BASED SYSTEM IDENTIFIC
Page 169: 5.3 OFF-LINE BASED SYSTEM IDENTIFIC
Page 177 and 178: 5.6 ON-LINE SYSTEM IDENTIFICATION 1
Page 179 and 180: 5.6 ON-LINE SYSTEM IDENTIFICATION 1
Page 181 and 182: 5.7 MODEL PERFORMANCE COMPARISON US
Page 183 and 184: 5.8 SUMMARY 151 methods such as wei
Page 185: 5.8 SUMMARY 153 would enable the im
Page 188 and 189: 156 CHAPTER 6 NEURAL NETWORK BASED
Page 215 and 216: Chapter 7 FLIGHT CONTROL SYSTEM DES
Page 217 and 218: 7.2 FLIGHT TESTS IMPLEMENTATION 185
Page 219 and 220: 7.3 EXPERIMENTAL RESULTS 187 1 0.8
Page 221 and 222:
7.3 EXPERIMENTAL RESULTS 189 Longit
Page 223 and 224:
7.3 EXPERIMENTAL RESULTS 191 Pitch
Page 225 and 226:
7.3 EXPERIMENTAL RESULTS 193 Flight
Page 227 and 228:
7.3 EXPERIMENTAL RESULTS 195 140 Ya
Page 229 and 230:
7.3 EXPERIMENTAL RESULTS 197 indica
Page 231 and 232:
7.3 EXPERIMENTAL RESULTS 199 20 100
Page 233 and 234:
7.3 EXPERIMENTAL RESULTS 201 Yaw Ra
Page 235 and 236:
7.3 EXPERIMENTAL RESULTS 203 mainta
Page 237 and 238:
7.3 EXPERIMENTAL RESULTS 205 Yaw Ra
Page 239:
7.4 SUMMARY 207 data measured from
Page 242 and 243:
210 CHAPTER 8 CONCLUSIONS AND FUTUR
Page 244 and 245:
212 CHAPTER 8 CONCLUSIONS AND FUTUR
Page 246 and 247:
214 REFERENCES B. W. Bequette. Non-
Page 248 and 249:
216 REFERENCES Konstantinos Dalamag
Page 250 and 251:
218 REFERENCES Wayne Johnson. Helic
Page 252 and 253:
220 REFERENCES B. Mettler, Mark B.
Page 254 and 255:
222 REFERENCES V. R. Puttige and S.
Page 256 and 257:
224 REFERENCES D.H. Shim. Hierarchi
Page 258 and 259:
226 REFERENCES Nikos Vitzilaios and
show all

The Development of Neural Network Based System Identification ...

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?