The Development of Neural Network Based System Identification ...

2.2 HELICOPTER DYNAMICS MODELLING AND SYSTEM IDENTIFICATION 21
Flight Control
System
Summation
of Forces,
Inertial Translational Velocities
u, v, w
Atmospheric
Motion
+
Main Rotor &
Stabiliser Bar
Tail Rotor
Kinematics
Gravity
Components
Euler
Angles
Fuselage
Engine/
Transmission
Summation of
Moments,
Inertial Rotational Velocities
p, q, r
Atmospheric
Motion
+
Empennage
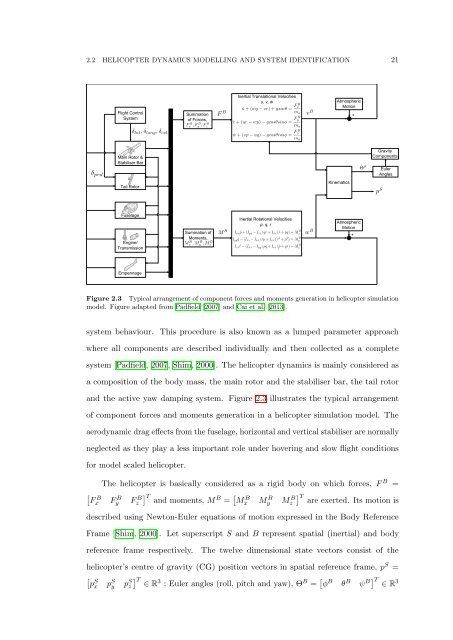
Figure 2.3 Typical arrangement of component forces and moments generation in helicopter simulation
model. Figure adapted from Padfield [2007] and Cai et al. [2013].
system behaviour. This procedure is also known as a lumped parameter approach
where all components are described individually and then collected as a complete
system [Padfield, 2007, Shim, 2000]. The helicopter dynamics is mainly considered as
a composition of the body mass, the main rotor and the stabiliser bar, the tail rotor
and the active yaw damping system. Figure 2.3 illustrates the typical arrangement
of component forces and moments generation in a helicopter simulation model. The
aerodynamic drag effects from the fuselage, horizontal and vertical stabiliser are normally
neglected as they play a less important role under hovering and slow flight conditions
for model scaled helicopter.
The helicopter is basically considered as a rigid body on which forces, F B =
[
F
B
x F B y F B z
] T and moments, M B = [ M B x M B y M B z
] T are exerted. Its motion is
described using Newton-Euler equations of motion expressed in the Body Reference
Frame [Shim, 2000]. Let superscript S and B represent spatial (inertial) and body
reference frame respectively.
The twelve dimensional state vectors consist of the
helicopter’s centre of gravity (CG) position vectors in spatial reference frame, p S =
[
p
S
x p S y p S ] T
z ∈ R 3 ; Euler angles (roll, pitch and yaw), Θ B = [ φ B θ B ψ B] T ∈ R
3