The Development of Neural Network Based System Identification ...

5.4 OFF-LINE BASED SYSTEM IDENTIFICATION FOR ELMAN NETWORK 141
Roll Rate, p (rad/s)
1.5
1
0.5
0
−0.5
data
Elman NNID
−1
0 100 200 300 400 500 600 700 800 900 1000
time (samples)
(a)
0.2
Prediction Error
0.1
0
−0.1
−0.2
0 100 200 300 400 500 600 700 800 900 1000
time (samples)
(b)
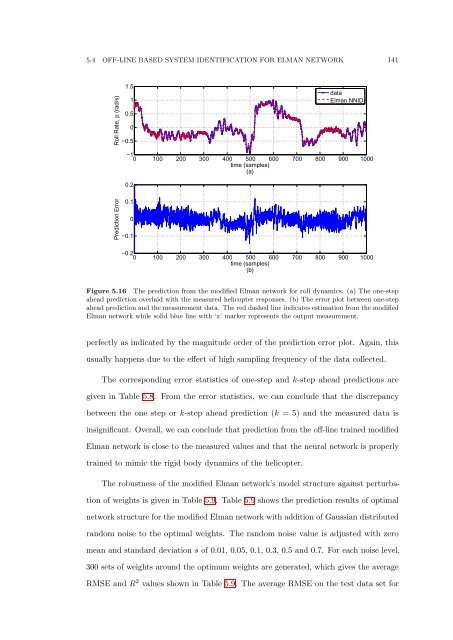
Figure 5.16 The prediction from the modified Elman network for roll dynamics. (a) The one-step
ahead prediction overlaid with the measured helicopter responses. (b) The error plot between one-step
ahead prediction and the measurement data. The red dashed line indicates estimation from the modified
Elman network while solid blue line with ‘x’ marker represents the output measurement.
perfectly as indicated by the magnitude order of the prediction error plot. Again, this
usually happens due to the effect of high sampling frequency of the data collected.
The corresponding error statistics of one-step and k-step ahead predictions are
given in Table 5.8. From the error statistics, we can conclude that the discrepancy
between the one step or k-step ahead prediction (k = 5) and the measured data is
insignificant. Overall, we can conclude that prediction from the off-line trained modified
Elman network is close to the measured values and that the neural network is properly
trained to mimic the rigid body dynamics of the helicopter.
The robustness of the modified Elman network’s model structure against perturbation
of weights is given in Table 5.9. Table 5.9 shows the prediction results of optimal
network structure for the modified Elman network with addition of Gaussian distributed
random noise to the optimal weights. The random noise value is adjusted with zero
mean and standard deviation s of 0.01, 0.05, 0.1, 0.3, 0.5 and 0.7. For each noise level,
300 sets of weights around the optimum weights are generated, which gives the average
RMSE and R 2 values shown in Table 5.9. The average RMSE on the test data set for