The significance of coherent flow structures for the turbulent mixing ...

ß
ß
6.2 Statistical properties of the buffer layer
6.2 Statistical properties of the buffer layer
6.2.1 Single point statistics
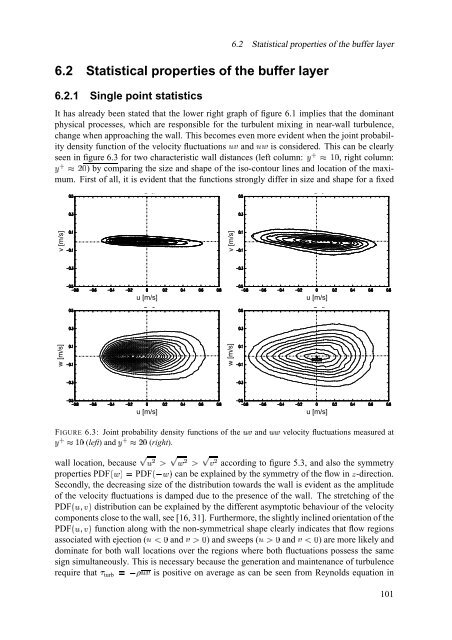
It has already been stated that the lower right graph of figure 6.1 implies that the dominant
physical processes, which are responsible for the turbulent mixing in near-wall turbulence,
change when approaching the wall. This becomes even more evident when the joint probabil-
is considered. This can be clearly
ity density function of the 697 velocity 69t
fluctuations
þ¥
and
seen in figure 6.3 for two characteristic wall distances u.v ;
(left column: , right column:
Ó ) by comparing the size and shape of the iso-contour lines and location of the maximum.
First of all, it is evident that the functions strongly differ in size and shape for a
u.v ;
fixed
v [m/s]
v [m/s]
u [m/s]
u [m/s]
w [m/s]
w [m/s]
u [m/s]
FIGURE 6.3: Joint probability density functions of /.0 the /3 and
(right).
(left) and Üvxwzy
u [m/s]
velocity fluctuations measured at
Üvxw ÷
wall location, K 6 ' £ K t ' £ K 7 ' because according to figure 5.3, and also the symmetry
PDF{|t~} W PDF{Ît~} properties can be explained by the symmetry of the flow X in -direction.
Secondly, the decreasing size of the distribution towards the wall is evident as the amplitude
of the velocity fluctuations is damped due to the presence of the wall. The stretching of the
7.} distribution can be explained by the different asymptotic behaviour of the velocity
PDF{6
components close to the wall, see [16, 31]. Furthermore, the slightly inclined orientation of the
function along with the non-symmetrical shape clearly indicates that flow regions
7.}
PDF{6
(6N€ 7 (6 £ € 7 £
W V Î& 6(7
associated with ejection and ) and sweeps and ) are more likely and
dominate for both wall locations over the regions where both fluctuations possess the same
sign simultaneously. This is necessary because the generation and maintenance of turbulence
require that turb is positive on average as can be seen from Reynolds equation in
101