Heiss W.D. (ed.) Quantum dots.. a doorway to - tiera.ru

146 C.W.J. Beenakker
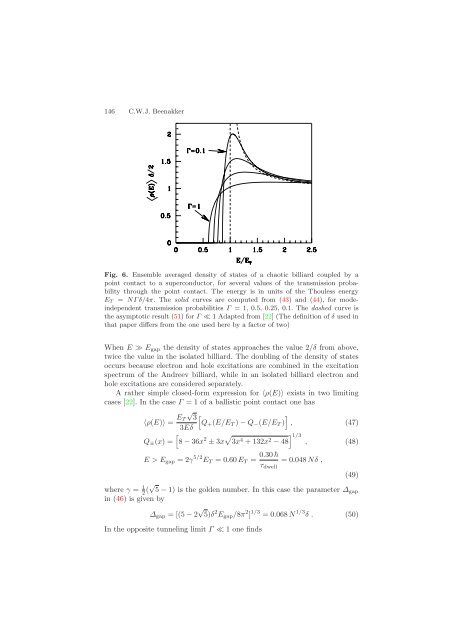
Fig. 6. Ensemble averaged density of states of a chaotic billiard coupled by a
point contact to a superconductor, for several values of the transmission probability
through the point contact. The energy is in units of the Thouless energy
ET = NΓδ/4π. The solid curves are computed from (43) and (44), for modeindependent
transmission probabilities Γ =1,0.5, 0.25, 0.1. The dashed curve is
the asymptotic result (51) for Γ ≪ 1 Adapted from [22] (The definition of δ used in
that paper differs from the one used here by a factor of two)
When E ≫ Egap the density of states approaches the value 2/δ from above,
twice the value in the isolated billiard. The doubling of the density of states
occurs because electron and hole excitations are combined in the excitation
spectrum of the Andreev billiard, while in an isolated billiard electron and
hole excitations are considered separately.
A rather simple closed-form expression for 〈ρ(E)〉 exists in two limiting
cases [22]. In the case Γ = 1 of a ballistic point contact one has
〈ρ(E)〉 = ET
√
3
�
�
Q+(E/ET ) − Q−(E/ET ) , (47)
3Eδ
�
Q±(x) = 8 − 36x 2 ± 3x � 3x4 + 132x2 �1/3 − 48 , (48)
E>Egap =2γ 5/2 ET =0.60 ET =
0.30 �
=0.048 Nδ ,
τdwell
(49)
where γ = 1
2 (√ 5 − 1) is the golden number. In this case the parameter ∆gap
in (46) is given by
∆gap = [(5 − 2 √ 5)δ 2 Egap/8π 2 ] 1/3 =0.068 N 1/3 δ. (50)
In the opposite tunneling limit Γ ≪ 1 one finds