universidad de chile dinámica de dominios en sistemas forzados ...

200
150
100
50
0
−50
−100
−150
−α ε
∆
∆ 0
−200
−2 −1 0 1 2 3 4 5
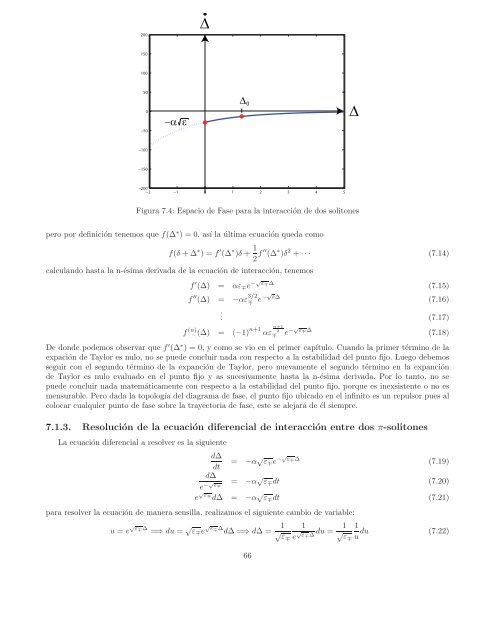
Figura 7.4: Espacio de Fase para la interacción de dos solitones
pero por definición tenemos que f(∆ ∗ ) = 0, así la última ecuación queda como
f(δ + ∆ ∗ ) = f ′ (∆ ∗ )δ + 1
2 f ′′ (∆ ∗ )δ 2 + · · · (7.14)
calculando hasta la n-ésima derivada de la ecuación de interacción, tenemos
f ′ (∆) = αε∓e −√ ε∓∆
f ′′ (∆) = −αε 3/2
∓ e−√ ε∆
∆
(7.15)
(7.16)
.
. (7.17)
f (n) (∆) = (−1) n+1 αε n+1
2
∓ e −√ε∓∆ (7.18)
De donde podemos observar que f ′ (∆ ∗ ) = 0, y como se vio en el primer capítulo. Cuando la primer término de la
expación de Taylor es nulo, no se puede concluir nada con respecto a la estabilidad del punto fijo. Luego debemos
seguir con el segundo término de la expanción de Taylor, pero nuevamente el segundo término en la expanción
de Taylor es nulo evaluado en el punto fijo y as sucesivamente hasta la n-ésima derivada. Por lo tanto, no se
puede concluir nada matemáticamente con respecto a la estabilidad del punto fijo, porque es inexsistente o no es
mensurable. Pero dada la topología del diagrama de fase, el punto fijo ubicado en el infinito es un repulsor pues al
colocar cualquier punto de fase sobre la trayectoria de fase, este se alejará de él siempre.
7.1.3. Resolución de la ecuación diferencial de interacción entre dos π-solitones
La ecuación diferencial a resolver es la siguiente
d∆
dt = −α√ε∓e −√ε∓∆ (7.19)
d∆
e−√ε∓ = −α√ e
ε∓dt (7.20)
√ ε∓d∆ √
= −α ε∓dt (7.21)
para resolver la ecuación de manera sensilla, realizamos el siguiente cambio de variable:
u = e √ ε∓∆ =⇒ du = √ ε∓e √ ε∓∆ d∆ =⇒ d∆ = 1
√ε∓
66
1
e √ 1
du = ε∓∆ √
ε∓
1
du (7.22)
u