universidad de chile dinámica de dominios en sistemas forzados ...
universidad de chile dinámica de dominios en sistemas forzados ...
universidad de chile dinámica de dominios en sistemas forzados ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
forma<br />
pero dado que ν es pequeño, t<strong>en</strong>emos<br />
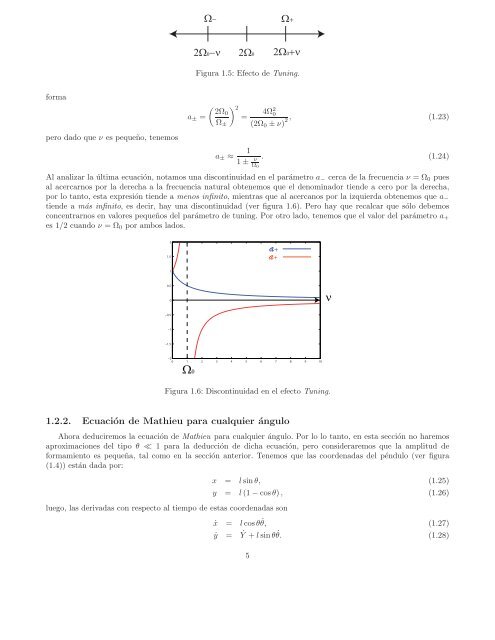
Ω− Ω+<br />
2Ω0−ν 2Ω0 2Ω0+ν<br />
Figura 1.5: Efecto <strong>de</strong> Tuning.<br />
<br />
2Ω0<br />
a± =<br />
Ω±<br />
a± ≈<br />
2<br />
=<br />
4Ω2 0<br />
2 , (1.23)<br />
(2Ω0 ± ν)<br />
1<br />
1 ± ν . (1.24)<br />
Ω0<br />
Al analizar la última ecuación, notamos una discontinuidad <strong>en</strong> el parámetro a− cerca <strong>de</strong> la frecu<strong>en</strong>cia ν = Ω0 pues<br />
al acercarnos por la <strong>de</strong>recha a la frecu<strong>en</strong>cia natural obt<strong>en</strong>emos que el <strong>de</strong>nominador ti<strong>en</strong><strong>de</strong> a cero por la <strong>de</strong>recha,<br />
por lo tanto, esta expresión ti<strong>en</strong><strong>de</strong> a m<strong>en</strong>os infinito, mi<strong>en</strong>tras que al acercanos por la izquierda obt<strong>en</strong>emos que a−<br />
ti<strong>en</strong><strong>de</strong> a más infinito, es <strong>de</strong>cir, hay una discontinuidad (ver figura 1.6). Pero hay que recalcar que sólo <strong>de</strong>bemos<br />
conc<strong>en</strong>trarnos <strong>en</strong> valores pequeños <strong>de</strong>l parámetro <strong>de</strong> tuning. Por otro lado, t<strong>en</strong>emos que el valor <strong>de</strong>l parámetro a+<br />
es 1/2 cuando ν = Ω0 por ambos lados.<br />
2<br />
1.5<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
−1.5<br />
a+<br />
a+<br />
−2<br />
0 1 2 3 4 5 6 7 8 9 10<br />
Ω0<br />
Figura 1.6: Discontinuidad <strong>en</strong> el efecto Tuning.<br />
1.2.2. Ecuación <strong>de</strong> Mathieu para cualquier ángulo<br />
Ahora <strong>de</strong>duciremos la ecuación <strong>de</strong> Mathieu para cualquier ángulo. Por lo lo tanto, <strong>en</strong> esta sección no haremos<br />
aproximaciones <strong>de</strong>l tipo θ ≪ 1 para la <strong>de</strong>ducción <strong>de</strong> dicha ecuación, pero consi<strong>de</strong>raremos que la amplitud <strong>de</strong><br />
formami<strong>en</strong>to es pequeña, tal como <strong>en</strong> la sección anterior. T<strong>en</strong>emos que las coor<strong>de</strong>nadas <strong>de</strong>l péndulo (ver figura<br />
(1.4)) están dada por:<br />
luego, las <strong>de</strong>rivadas con respecto al tiempo <strong>de</strong> estas coor<strong>de</strong>nadas son<br />
ν<br />
x = l sin θ, (1.25)<br />
y = l (1 − cosθ), (1.26)<br />
˙x = l cosθ ˙ θ, (1.27)<br />
˙y = ˙ Y + l sinθ ˙ θ. (1.28)<br />
5