ComputerAided_Design_Engineering_amp_Manufactur.pdf

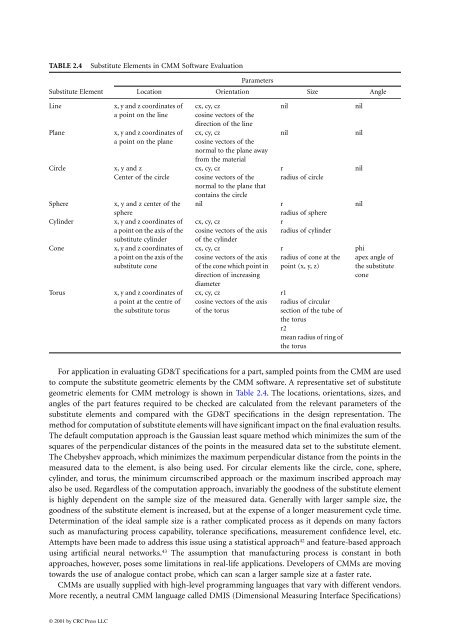
TABLE 2.4 Substitute Elements in CMM Software Evaluation
Substitute Element
Line x, y and z coordinates of
a point on the line
Plane x, y and z coordinates of
a point on the plane
Circle x, y and z
Center of the circle
Sphere x, y and z center of the
sphere
Cylinder x, y and z coordinates of
a point on the axis of the
substitute cylinder
Cone x, y and z coordinates of
a point on the axis of the
substitute cone
Torus x, y and z coordinates of
a point at the centre of
the substitute torus
For application in evaluating GD&T specifications for a part, sampled points from the CMM are used
to compute the substitute geometric elements by the CMM software. A representative set of substitute
geometric elements for CMM metrology is shown in Table 2.4. The locations, orientations, sizes, and
angles of the part features required to be checked are calculated from the relevant parameters of the
substitute elements and compared with the GD&T specifications in the design representation. The
method for computation of substitute elements will have significant impact on the final evaluation results.
The default computation approach is the Gaussian least square method which minimizes the sum of the
squares of the perpendicular distances of the points in the measured data set to the substitute element.
The Chebyshev approach, which minimizes the maximum perpendicular distance from the points in the
measured data to the element, is also being used. For circular elements like the circle, cone, sphere,
cylinder, and torus, the minimum circumscribed approach or the maximum inscribed approach may
also be used. Regardless of the computation approach, invariably the goodness of the substitute element
is highly dependent on the sample size of the measured data. Generally with larger sample size, the
goodness of the substitute element is increased, but at the expense of a longer measurement cycle time.
Determination of the ideal sample size is a rather complicated process as it depends on many factors
such as manufacturing process capability, tolerance specifications, measurement confidence level, etc.
Attempts have been made to address this issue using a statistical approach 42 and feature-based approach
using artificial neural networks. 43 The assumption that manufacturing process is constant in both
approaches, however, poses some limitations in real-life applications. Developers of CMMs are moving
towards the use of analogue contact probe, which can scan a larger sample size at a faster rate.
CMMs are usually supplied with high-level programming languages that vary with different vendors.
More recently, a neutral CMM language called DMIS (Dimensional Measuring Interface Specifications)
© 2001 by CRC Press LLC
Location
Parameters
Orientation Size Angle
cx, cy, cz
cosine vectors of the
direction of the line
cx, cy, cz
cosine vectors of the
normal to the plane away
from the material
cx, cy, cz
cosine vectors of the
normal to the plane that
contains the circle
nil nil
nil nil
r
radius of circle
nil r
radius of sphere
cx, cy, cz
r
cosine vectors of the axis radius of cylinder
of the cylinder
cx, cy, cz
r
cosine vectors of the axis radius of cone at the
of the cone which point in point (x, y, z)
direction of increasing
diameter
cx, cy, cz
r1
cosine vectors of the axis radius of circular
of the torus
section of the tube of
the torus
r2
mean radius of ring of
the torus
nil
nil
phi
apex angle of
the substitute
cone