Contents - Max-Planck-Institut für Physik komplexer Systeme

Dynamic force clamp. In collaboration with J. Barral
and P. Martin (Insitut Curie, Paris) we developed an
experimental setup to adress the problem [9]. It was
technically not feasible to interconnect biological hair
bundles with elastic linkages. Therefore, we opted for
a hybrid approach in which we coupled a biological
hair bundle to two virtual hair bundles (”cyber clones”)
simulated in real-time on a computer (see Fig. 1). More
specifically, in each time step (update rate 2.5kHz), we
(i) monitored the position of the hair bundle, (ii) calculated
the coupling forces acting on the hair bundle
and the virtual cyber clones, (ii) exerted the force on
the hair bundle by means of a flexible glass fiber, and
(iv) integrated the stochastic differential equations describing
cyber-clone dynamics (including the respective
coupling forces) to generate the new positions of
the virtual bundles. By means of this novel dynamic
force clamp, we were thus able to emulate a situation in
which a biological hair bundle under study was elastically
coupled to two neighboring hair bundles of similar
characteristics.
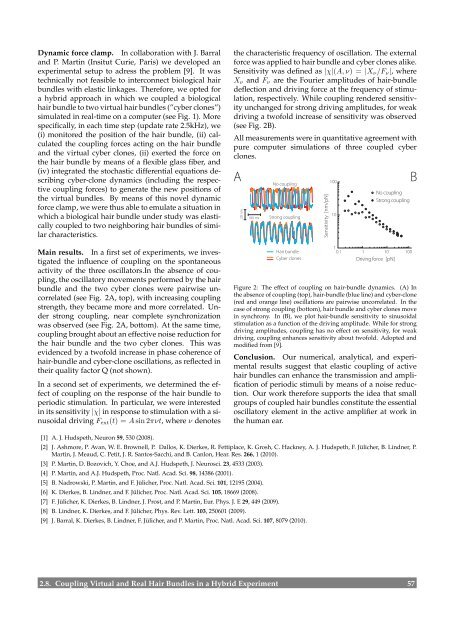
Main results. In a first set of experiments, we investigated
the influence of coupling on the spontaneous
activity of the three oscillators.In the absence of coupling,
the oscillatory movements performed by the hair
bundle and the two cyber clones were pairwise uncorrelated
(see Fig. 2A, top), with increasing coupling
strength, they became more and more correlated. Under
strong coupling, near complete synchronization
was observed (see Fig. 2A, bottom). At the same time,
coupling brought about an effective noise reduction for
the hair bundle and the two cyber clones. This was
evidenced by a twofold increase in phase coherence of
hair-bundle and cyber-clone oscillations, as reflected in
their quality factor Q (not shown).
In a second set of experiments, we determined the effect
of coupling on the response of the hair bundle to
periodic stimulation. In particular, we were interested
in its sensitivity |χ| in response to stimulation with a sinusoidal
driving Fext(t) = Asin 2πνt, where ν denotes
[1] A. J. Hudspeth, Neuron 59, 530 (2008).
the characteristic frequency of oscillation. The external
force was applied to hair bundle and cyber clones alike.
Sensitivity was defined as |χ|(A,ν) = |Xν/Fν|, where
Xν and Fν are the Fourier amplitudes of hair-bundle
deflection and driving force at the frequency of stimulation,
respectively. While coupling rendered sensitivity
unchanged for strong driving amplitudes, for weak
driving a twofold increase of sensitivity was observed
(see Fig. 2B).
All measurements were in quantitative agreement with
pure computer simulations of three coupled cyber
clones.
A B
20 nm
100 ms
No coupling
Strong coupling
Hair bundle
Cyber clones
Sensitivity [nm/pN]
100
10
No coupling
Strong coupling
1
0.1 1 10 100
Driving force [pN]
Figure 2: The effect of coupling on hair-bundle dynamics. (A) In
the absence of coupling (top), hair-bundle (blue line) and cyber-clone
(red and orange line) oscillations are pairwise uncorrelated. In the
case of strong coupling (bottom), hair bundle and cyber clones move
in synchrony. In (B), we plot hair-bundle sensitivity to sinusoidal
stimulation as a function of the driving amplitude. While for strong
driving amplitudes, coupling has no effect on sensitivity, for weak
driving, coupling enhances sensitivity about twofold. Adopted and
modified from [9].
Conclusion. Our numerical, analytical, and experimental
results suggest that elastic coupling of active
hair bundles can enhance the transmission and amplification
of periodic stimuli by means of a noise reduction.
Our work therefore supports the idea that small
groups of coupled hair bundles constitute the essential
oscillatory element in the active amplifier at work in
the human ear.
[2] J. Ashmore, P. Avan, W. E. Brownell, P. Dallos, K. Dierkes, R. Fettiplace, K. Grosh, C. Hackney, A. J. Hudspeth, F. Jülicher, B. Lindner, P.
Martin, J. Meaud, C. Petit, J. R. Santos-Sacchi, and B. Canlon, Hear. Res. 266, 1 (2010).
[3] P. Martin, D. Bozovich, Y. Choe, and A.J. Hudspeth, J. Neurosci. 23, 4533 (2003).
[4] P. Martin, and A.J. Hudspeth, Proc. Natl. Acad. Sci. 98, 14386 (2001).
[5] B. Nadrowski, P. Martin, and F. Jülicher, Proc. Natl. Acad. Sci. 101, 12195 (2004).
[6] K. Dierkes, B. Lindner, and F. Jülicher, Proc. Natl. Acad. Sci. 105, 18669 (2008).
[7] F. Jülicher, K. Dierkes, B. Lindner, J. Prost, and P. Martin, Eur. Phys. J. E 29, 449 (2009).
[8] B. Lindner, K. Dierkes, and F. Jülicher, Phys. Rev. Lett. 103, 250601 (2009).
[9] J. Barral, K. Dierkes, B. Lindner, F. Jülicher, and P. Martin, Proc. Natl. Acad. Sci. 107, 8079 (2010).
2.8. Coupling Virtual and Real Hair Bundles in a Hybrid Experiment 57