Contents - Max-Planck-Institut für Physik komplexer Systeme

agents following the respective strategy.
n C
n C
n C
0.4
0.3
0.4
0.3
p = 0.8
300 350 400
1
0.5
p = 0.1
p = 0.98
0
0 1000 2000 3000
t
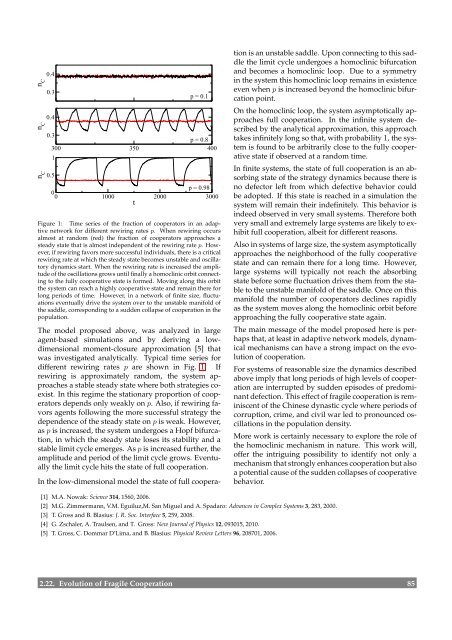
Figure 1: Time series of the fraction of cooperators in an adaptive
network for different rewiring rates p. When rewiring occurs
almost at random (red) the fraction of cooperators approaches a
steady state that is almost independent of the rewiring rate p. However,
if rewiring favors more successful individuals, there is a critical
rewiring rate at which the steady state becomes unstable and oscillatory
dynamics start. When the rewiring rate is increased the amplitude
of the oscillations grows until finally a homoclinic orbit connecting
to the fully cooperative state is formed. Moving along this orbit
the system can reach a highly cooperative state and remain there for
long periods of time. However, in a network of finite size, fluctuations
eventually drive the system over to the unstable manifold of
the saddle, corresponding to a sudden collapse of cooperation in the
population.
The model proposed above, was analyzed in large
agent-based simulations and by deriving a lowdimensional
moment-closure approximation [5] that
was investigated analytically. Typical time series for
different rewiring rates p are shown in Fig. 1. If
rewiring is approximately random, the system approaches
a stable steady state where both strategies coexist.
In this regime the stationary proportion of cooperators
depends only weakly on p. Also, if rewiring favors
agents following the more successful strategy the
dependence of the steady state on p is weak. However,
as p is increased, the system undergoes a Hopf bifurcation,
in which the steady state loses its stability and a
stable limit cycle emerges. As p is increased further, the
amplitude and period of the limit cycle grows. Eventually
the limit cycle hits the state of full cooperation.
In the low-dimensional model the state of full coopera-
[1] M.A. Nowak: Science 314, 1560, 2006.
tion is an unstable saddle. Upon connecting to this saddle
the limit cycle undergoes a homoclinic bifurcation
and becomes a homoclinic loop. Due to a symmetry
in the system this homoclinic loop remains in existence
even when p is increased beyond the homoclinic bifurcation
point.
On the homoclinic loop, the system asymptotically approaches
full cooperation. In the infinite system described
by the analytical approximation, this approach
takes infinitely long so that, with probability 1, the system
is found to be arbitrarily close to the fully cooperative
state if observed at a random time.
In finite systems, the state of full cooperation is an absorbing
state of the strategy dynamics because there is
no defector left from which defective behavior could
be adopted. If this state is reached in a simulation the
system will remain their indefinitely. This behavior is
indeed observed in very small systems. Therefore both
very small and extremely large systems are likely to exhibit
full cooperation, albeit for different reasons.
Also in systems of large size, the system asymptotically
approaches the neighborhood of the fully cooperative
state and can remain there for a long time. However,
large systems will typically not reach the absorbing
state before some fluctuation drives them from the stable
to the unstable manifold of the saddle. Once on this
manifold the number of cooperators declines rapidly
as the system moves along the homoclinic orbit before
approaching the fully cooperative state again.
The main message of the model proposed here is perhaps
that, at least in adaptive network models, dynamical
mechanisms can have a strong impact on the evolution
of cooperation.
For systems of reasonable size the dynamics described
above imply that long periods of high levels of cooperation
are interrupted by sudden episodes of predominant
defection. This effect of fragile cooperation is reminiscent
of the Chinese dynastic cycle where periods of
corruption, crime, and civil war led to pronounced oscillations
in the population density.
More work is certainly necessary to explore the role of
the homoclinic mechanism in nature. This work will,
offer the intriguing possibility to identify not only a
mechanism that strongly enhances cooperation but also
a potential cause of the sudden collapses of cooperative
behavior.
[2] M.G. Zimmermann, V.M. Eguiluz,M. San Miguel and A. Spadaro: Advances in Complex Systems 3, 283, 2000.
[3] T. Gross and B. Blasius: J. R. Soc. Interface 5, 259, 2008.
[4] G. Zschaler, A. Traulsen, and T. Gross: New Journal of Physics 12, 093015, 2010.
[5] T. Gross, C. Dommar D’Lima, and B. Blasius: Physical Review Letters 96, 208701, 2006.
2.22. Evolution of Fragile Cooperation 85