Contents - Max-Planck-Institut für Physik komplexer Systeme

2.24 Pattern Formation in Active Fluids
JUSTIN S. BOIS, FRANK JÜLICHER, STEPHAN W. GRILL
Active stresses are exerted in cells and tissues by motor
protein-driven contraction of the cytoskeleton. Concurrently,
chemical species are reacting and diffusing
within the material. Reaction-diffusion mechanisms
have long been implicated in biological pattern formation
of chemical species, but mechanical stresses are
also crucial for developmental processes [1]. The active
stress and distribution of chemical species associated
with pattern formation are coupled in two ways. First,
the active stress is under control of biochemical regulators
affecting motor activity and actin polymerization,
which may themselves diffuse and undergo chemical
reactions. Secondly, the flow of contractile material
transports chemical species by advection. In this
work [2], we developed a new framework for biological
pattern formation considering these two forms of
coupling.
In this first simplified treatment, we treat a contracting
cytoskeleton or tissue as a thin film of an active viscous
fluid and consider only movements in the x-direction.
The equation of motion is then [3, 4]
∂x ζ∆µ(c) = −η∂ 2 x v + γ v,
where v is the fluid flow velocity, η is the viscosity, γ
is a friction coefficient that takes into account boundary
stresses, and ζ∆µ is the active stress, dependent on
the concentrations of chemical species, c ≡ (c1,...,cn).
The equation of motion reveals a physical length scale
of the system, ℓ ≡ η/γ, which is the decay length of
fluid velocity in response to a local active stress gradient
[4]. In addition, mass conservation gives
∂t ci = Di ∂ 2 x ci + Ri(c) − ∂x(ci v) ∀i ∈ [1,n],
where Di is the diffusivity of species i and Ri(c) is the
rate of production of species i by chemical reaction. The
last term accounts for advective transport of species i
that occurs by virtue of bulk fluid motion. The relevant
dimensionless parameters are the ratio of diffusivities,
Di/D1, and the Péclet number Pe ≡ (ζ∆µ)0 /γD1,
where (ζ∆µ)0 is the maximal possible active stress.
The Péclet number is the ratio of diffusive to advective
times scales and is therefore a measure of the relative
importance of advection in the system dynamics. Additionally,
the functional forms of Ri(c) and ζ∆µ(c), as
well as the dimensionless length of the system L/ℓ (the
ratio of the total system extent to the hydrodynamic
length), are important for the dynamics.
Case study 1: active stress-driven instabilities. As
a first case study, we consider a single biochemical
species with concentration c that regulates active stress
(a) (b)
1
0
¢2¢1
2£D¤(k)
increasing
Pe
k¡
0 1 2 3
c 0
10 2
10 1
10 0
10 -1
10 0 10 -2
no patterns
pattern-forming
region
10 1
Pe/(1 +(¥¦¡/L) 2 )
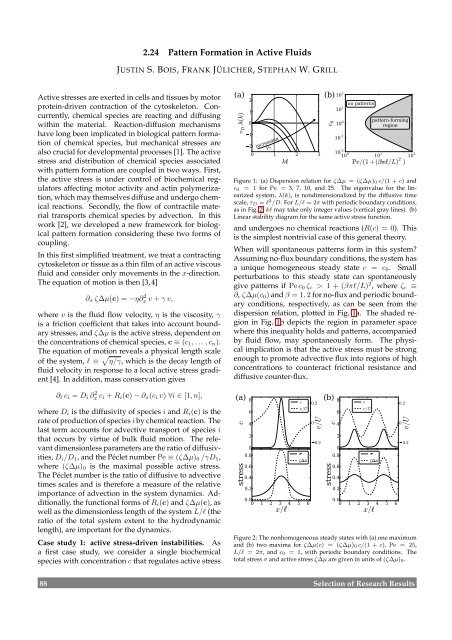
Figure 1: (a) Dispersion relation for ζ∆µ = (ζ∆µ)0 c/(1 + c) and
c0 = 1 for Pe = 3, 7, 10, and 25. The eigenvalue for the linearized
system, λ(k), is nondimensionalized by the diffusive time
scale, τD = ℓ 2 /D. For L/ℓ = 2π with periodic boundary conditions,
as in Fig. 2, kℓ may take only integer values (vertical gray lines). (b)
Linear stability diagram for the same active stress function.
and undergoes no chemical reactions (R(c) = 0). This
is the simplest nontrivial case of this general theory.
When will spontaneous patterns form in this system?
Assuming no-flux boundary conditions, the system has
a unique homogeneous steady state c = c0. Small
perturbations to this steady state can spontaneously
give patterns if Pe c0 ζc > 1 + (βπℓ/L) 2 , where ζc ≡
∂c ζ∆µ(c0) and β = 1,2 for no-flux and periodic boundary
conditions, respectively, as can be seen from the
dispersion relation, plotted in Fig. 1a. The shaded region
in Fig. 1b depicts the region in parameter space
where this inequality holds and patterns, accompanied
by fluid flow, may spontaneously form. The physical
implication is that the active stress must be strong
enough to promote advective flux into regions of high
concentrations to counteract frictional resistance and
diffusive counter-flux.
(a)
c
stress
8
6
4
2
0
0.8
0.6
0.4
0.2
0 1 2 3 4 5
x/§
0.0
6
c
v/U
0.2
v/U
0
(b)
c
2
0.2 ¨©0 0.8
0.6
stress
8
6
4
0.4
0.2
c
v/U
0.2
v/U
0.2
10 2
¨©
x/§
0.0
0 1 2 3 4 5 6
Figure 2: The nonhomogeneous steady states with (a) one maximum
and (b) two maxima for ζ∆µ(c) = (ζ∆µ)0 c/(1 + c), Pe = 25,
L/ℓ = 2π, and c0 = 1, with periodic boundary conditions. The
total stress σ and active stress ζ∆µ are given in units of (ζ∆µ)0.
88 Selection of Research Results
0