Skript zur Topologie 1 - M10

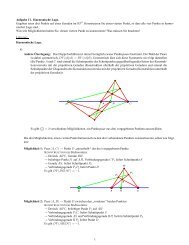
TOPOLOGIE I 3
Die Homologiegruppen einzuführen wird zwar einige Zeit in Anspruch
nehmen. Wenn sie einmal zur Verfügung stehen, ist der Umgang mit ihnen
allerdings sehr bequem und viele schöne Sätze können wir mit ihrer Hilfe
beweisen. Neben obigen Tatsachen, erwähne ich den Jordanschen Kurvensatz
Satz 1.2. Es sei f : S n−1 → R n eine topologische Einbettung (d.h. f ist
stetig und injektiv). Dann besteht R n \f(S n−1 ) aus genau zwei Komponenten,
wobei genau eine beschränkt und eine unbeschränkt ist.
Eine weitere wichtige Anwendung ist der Satz von Borsuk-Ulam:
Satz 1.3. Es sei f : S n → R n eine stetige Abbildung. Dann existiert ein
Punkt x ∈ S n mit f(x) = f(−x).
Des weiteren werden wir eine wichtige Invariante, die Eulercharakteristik
eines Simplizialkomplexes untersuchen und die Eulersche Polyederformel beweisen:
Satz 1.4. In einem konvexen Polyeder im R 3 gilt für die Anzahl e der Ecken,
k der Kanten und f der Flächen die Formel
e − k + f = 2 .
Das schöne an dieses Anwendungen ist, dass die Homologietheorie zwar
für den Beweis eine entscheidende Rolle spielt, aber in den Sätzen selbst
nicht vorkommt.
Homologiegruppen kann man insbesondere für simpliziale Komplexe und
sogenannten CW -Komplexe effektiv berechnen. Wir werden diese Klassen
von Räumen ausführlich diskutieren. Während der Diskussion der Homologiegruppen
werden wir parallel einige Grundlagen der homologischen Algebra
entwickeln.
Die Homotopiegruppen sind einfacher zu definieren als Homologiegruppen
und in gewisse Hinsicht die grundlegenderen Invarianten. Allerdings sind sie
viel schwerer zu berechnen als Homologiegruppen und zum Beispiel für keine
der Sphären S n mit n ≥ 2 vollständig bekannt. Die Bordismusgruppen
schlagen eine Brücke zur Differenzialtopologie, d.h. zur Untersuchung differenzierbarer
Mannigfaltigkeiten. Diese liefern einerseits viel Beispielmaterial
für die Anwendung der Homologietheorie, gestatten es aber andererseits
auch, das interessante Wechselspiel von differentialtopologischen Methoden
(insbesondere Transversalität) und Methoden aus der Homologie- und Homotopietheorie
zu studieren.
Heutzutage ist die algebraische Topologie eine hochentwickelte Theorie
mit zahlreichen Bezügen zur Differentialgeomtrie, zur algebraischen Geometrie
und zur Algebra.
2. Simpliziale und singuläre Homologie
Bevor wir Homologiegruppen für beliebige topologische Räume definieren,
veranschaulichen wir zunächst die wesentliche Idee im speziellen Fall der