The international economics of resources and resource ... - Index of

332 F. Beckenbach, R. Briegel
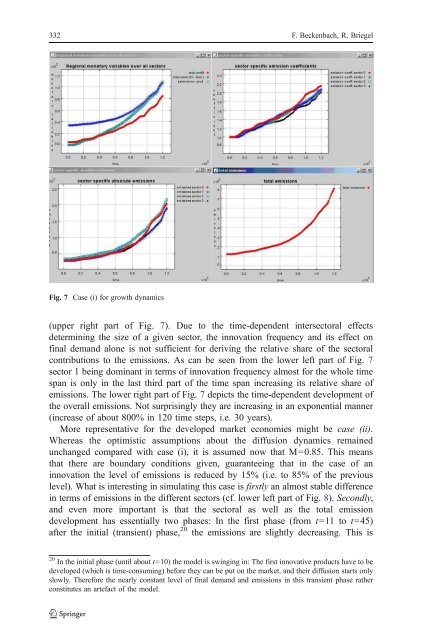
Fig. 7 Case (i) for growth dynamics
(upper right part of Fig. 7). Due to the time-dependent intersectoral effects
determining the size of a given sector, the innovation frequency and its effect on
final demand alone is not sufficient for deriving the relative share of the sectoral
contributions to the emissions. As can be seen from the lower left part of Fig. 7
sector 1 being dominant in terms of innovation frequency almost for the whole time
span is only in the last third part of the time span increasing its relative share of
emissions. The lower right part of Fig. 7 depicts the time-dependent development of
the overall emissions. Not surprisingly they are increasing in an exponential manner
(increase of about 800% in 120 time steps, i.e. 30 years).
More representative for the developed market economies might be case (ii).
Whereas the optimistic assumptions about the diffusion dynamics remained
unchanged compared with case (i), it is assumed now that M=0.85. This means
that there are boundary conditions given, guaranteeing that in the case of an
innovation the level of emissions is reduced by 15% (i.e. to 85% of the previous
level). What is interesting in simulating this case is firstly an almost stable difference
in terms of emissions in the different sectors (cf. lower left part of Fig. 8). Secondly,
and even more important is that the sectoral as well as the total emission
development has essentially two phases: In the first phase (from t=11 to t=45)
after the initial (transient) phase, 20 the emissions are slightly decreasing. This is
20 In the initial phase (until about t=10) the model is swinging in: The first innovative products have to be
developed (which is time-consuming) before they can be put on the market, and their diffusion starts only
slowly. Therefore the nearly constant level of final demand and emissions in this transient phase rather
constitutes an artefact of the model.