Phase-field modeling of diffusion controlled phase ... - KTH Mechanics

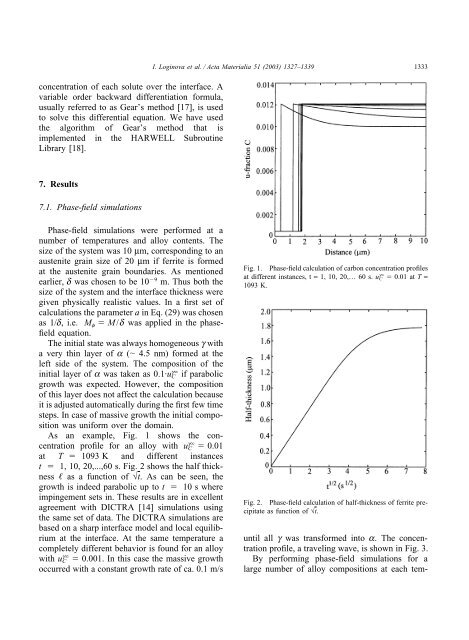
I. Loginova et al. / Acta Materialia 51 (2003) 1327–13391333concentration of each solute over the interface. Avariable order backward differentiation formula,usually referred to as Gear’s method [17], is usedto solve this differential equation. We have usedthe algorithm of Gear’s method that isimplemented in the HARWELL SubroutineLibrary [18].7. Results7.1. Phase-field simulationsPhase-field simulations were performed at anumber of temperatures and alloy contents. Thesize of the system was 10 µm, corresponding to anaustenite grain size of 20 µm if ferrite is formedat the austenite grain boundaries. As mentionedearlier, d was chosen to be 10 9 m. Thus both thesize of the system and the interface thickness weregiven physically realistic values. In a first set ofcalculations the parameter a in Eq. (29) was chosenas 1/d, i.e. M f M/d was applied in the phasefieldequation.The initial state was always homogeneous g witha very thin layer of a ( 4.5 nm) formed at theleft side of the system. The composition of theinitial layer of a was taken as 0.1·uCg if parabolicgrowth was expected. However, the compositionof this layer does not affect the calculation becauseit is adjusted automatically during the first few timesteps. In case of massive growth the initial compositionwas uniform over the domain.As an example, Fig. 1 shows the concentrationprofile for an alloy with u gC 0.01at T 1093 K and different instancest 1, 10, 20,...,60 s. Fig. 2 shows the half thickness as a function of √t. As can be seen, thegrowth is indeed parabolic up to t 10 s whereimpingement sets in. These results are in excellentagreement with DICTRA [14] simulations usingthe same set of data. The DICTRA simulations arebased on a sharp interface model and local equilibriumat the interface. At the same temperature acompletely different behavior is found for an alloywith uCg 0.001. In this case the massive growthoccurred with a constant growth rate of ca. 0.1 m/sFig. 1. Phase-field calculation of carbon concentration profilesat different instances, t = 1, 10, 20,… 60 s. u gC 0.01 at T =1093 K.Fig. 2. Phase-field calculation of half-thickness of ferrite precipitateas function of √t.until all g was transformed into a. The concentrationprofile, a traveling wave, is shown in Fig. 3.By performing phase-field simulations for alarge number of alloy compositions at each tem-