Phase-field modeling of diffusion controlled phase ... - KTH Mechanics

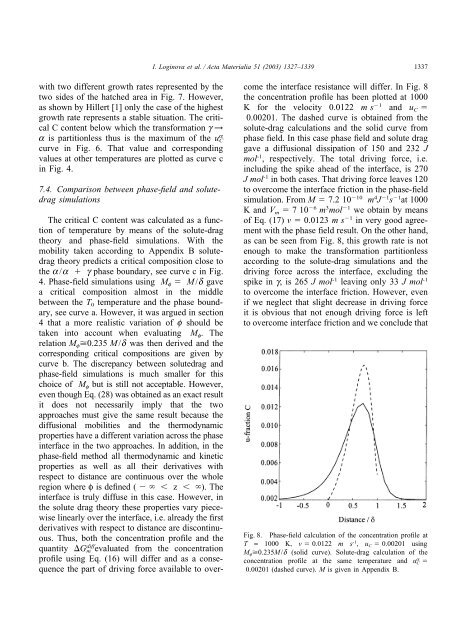
I. Loginova et al. / Acta Materialia 51 (2003) 1327–13391337with two different growth rates represented by thetwo sides of the hatched area in Fig. 7. However,as shown by Hillert [1] only the case of the highestgrowth rate represents a stable situation. The criticalC content below which the transformation g →a is partitionless thus is the maximum of the u a Ccurve in Fig. 6. That value and correspondingvalues at other temperatures are plotted as curve cin Fig. 4.7.4. Comparison between phase-field and solutedragsimulationsThe critical C content was calculated as a functionof temperature by means of the solute-dragtheory and phase-field simulations. With themobility taken according to Appendix B solutedragtheory predicts a critical composition close tothe a/a g phase boundary, see curve c in Fig.4. Phase-field simulations using M f M/d gavea critical composition almost in the middlebetween the T 0 temperature and the phase boundary,see curve a. However, it was argued in section4 that a more realistic variation of f should betaken into account when evaluating M f . Therelation M f 0.235 M/d was then derived and thecorresponding critical compositions are given bycurve b. The discrepancy between solutedrag andphase-field simulations is much smaller for thischoice of M f but is still not acceptable. However,even though Eq. (28) was obtained as an exact resultit does not necessarily imply that the twoapproaches must give the same result because thediffusional mobilities and the thermodynamicproperties have a different variation across the phaseinterface in the two approaches. In addition, in thephase-field method all thermodynamic and kineticproperties as well as all their derivatives withrespect to distance are continuous over the wholeregion where φ is defined ( z ). Theinterface is truly diffuse in this case. However, inthe solute drag theory these properties vary piecewiselinearly over the interface, i.e. already the firstderivatives with respect to distance are discontinuous.Thus, both the concentration profile and thequantity G diffm evaluated from the concentrationprofile using Eq. (16) will differ and as a consequencethe part of driving force available to overcomethe interface resistance will differ. In Fig. 8the concentration profile has been plotted at 1000K for the velocity 0.0122 ms 1 and u C 0.00201. The dashed curve is obtained from thesolute-drag calculations and the solid curve fromphase field. In this case phase field and solute draggave a diffusional dissipation of 150 and 232 Jmol -1 , respectively. The total driving force, i.e.including the spike ahead of the interface, is 270Jmol -1 in both cases. That driving force leaves 120to overcome the interface friction in the phase-fieldsimulation. From M 7.2 10 10 m 4 J 1 s 1 at 1000K and V m 710 6 m 3 mol 1 we obtain by meansof Eq. (17) v 0.0123 ms 1 in very good agreementwith the phase field result. On the other hand,as can be seen from Fig. 8, this growth rate is notenough to make the transformation partitionlessaccording to the solute-drag simulations and thedriving force across the interface, excluding thespike in g, is 265 Jmol -1 leaving only 33 Jmol -1to overcome the interface friction. However, evenif we neglect that slight decrease in driving forceit is obvious that not enough driving force is leftto overcome interface friction and we conclude thatFig. 8. Phase-field calculation of the concentration profile atT = 1000 K, v 0.0122 m s -1 , u C 0.00201 usingM f 0.235M/d (solid curve). Solute-drag calculation of theconcentration profile at the same temperature and u a C 0.00201 (dashed curve). M is given in Appendix B.