UWE Bristol Engineering showcase 2015

Billy Nightingale
BEng (Hons) Motorsport Engineering
Project Supervisor
John Kamalu
Reducing the Fatigue of Mountain Bike Rider
Introduction
The project was approximately weight 70% theoretical analysis and 30%
practical. The overall focus of this study is to determine if the vibrations
transmitted from rough trail conditions contribute to the phenomenon
known as arm pump, this will be achieved through experiments. Arm
pump is when the muscles within the forearm closes around the blood
vessels and causes the arm to fatigue. The the suspension
system will be mathematically model as a one degree of
freedom model to analysis the theoretical response and
improve the suspension system. To understand the response
of the system the variables that make up the suspension
system must be understood such as spring stiffness k, damping
coefficient c, the natural angular frequency ωω oo and of course the mass m.
These variables will also be found through experimental work as well as
numerical calculations. MATLAB will be used to create an easily adjustable
code that will produce the response of the system graphically and
numerically. The refinement of the suspension system will be done for two
disciplines; downhill riding and cross country, they will improve the
handling and reduce excessive vibration above 2 m/s-2, which is the
exposure limit determined through literature.
Mathematical Modelling
With the computational aid of MATLAB. three methods were used to excite
the suspension system and determine the response, these were; the
response of the suspensions system due to an initial displacement of the
mountain bike and rider from equilibrium, the response of the suspension
system after an applied force, the response of the suspension system
under harmonic motion of the base. These three methods can be defined
by the equations shown below in order;
xx tt = ee −ζζωω oott
xx oo cos ωω dd tt + ẋ oo+ζζωω oo xx oo
ωω dd
sin ωω dd tt
When dealing with vibration responses there are three main characteristic, that
make up the response of an oscillating structure displacement which has just
been given in the above equations, acceleration and velocity. The mathematics at
this point becomes far more complex the derivative of displacement gives velocity
and the derivative of velocity gives acceleration, hence these equations must be
derived to fully understand the response of a mountain bike due to an excitation.
Free Damped Response Acceleration vs Time
These equations were derived and a code In
c=400.85 k=40449.4 c=500 k=40449.4 c=400.85 k=50000
MATLAB was created. Which was used to
c=800 k=40449.4 c=1000 k=40449.4 c=700 k=40449.4
c=400.85 k=40000 c=400.85 k=35000 c=600 k=40449.4
refine the suspension system.
15.00
The signal from field
10.00
5.00
experiments were
0.00
transformed using
-5.00
Fast Fourier Transform
-10.00
transform experiments.
-15.00
Experiments
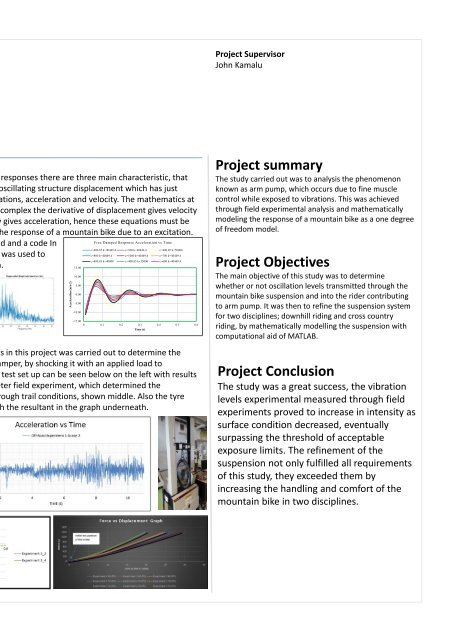
One of the many experiments in this project was carried out to determine the
damping ratio of the front damper, by shocking it with an applied load to
determine the response, the test set up can be seen below on the left with results
underneath. The accelerometer field experiment, which determined the
transmitted vibrations from rough trail conditions, shown middle. Also the tyre
stiffness test on the right with the resultant in the graph underneath.
Acceleration (m/s-2)
0 0.1 0.2 0.3 0.4 0.5 0.6
Time (s)
Project summary
The study carried out was to analysis the phenomenon
known as arm pump, which occurs due to fine muscle
control while exposed to vibrations. This was achieved
through field experimental analysis and mathematically
modeling the response of a mountain bike as a one degree
of freedom model.
Project Objectives
The main objective of this study was to determine
whether or not oscillation levels transmitted through the
mountain bike suspension and into the rider contributing
to arm pump. It was then to refine the suspension system
for two disciplines; downhill riding and cross country
riding, by mathematically modelling the suspension with
computational aid of MATLAB.
Project Conclusion
The study was a great success, the vibration
levels experimental measured through field
experiments proved to increase in intensity as
surface condition decreased, eventually
surpassing the threshold of acceptable
exposure limits. The refinement of the
suspension not only fulfilled all requirements
of this study, they exceeded them by
increasing the handling and comfort of the
mountain bike in two disciplines.
xx tt = FF oo
KK (1 − ee−ζζωω oott (cos(ωω dd tt) + ζζωω oo
ωω dd
sin(ωω dd tt))
xx pp tt = XXXXXXXX(ωωωω − φφ) where X is give by XX YY = [ 1+(2ζζζζ) 2
(1−rr 2 ) 2 +(2ζζζζ) 2]1/2