Kleine Einführung in die Astronavigation und Astronomie 1 Einleitung

45
40
35
-30 -25 -20 -15 -10 -5 0
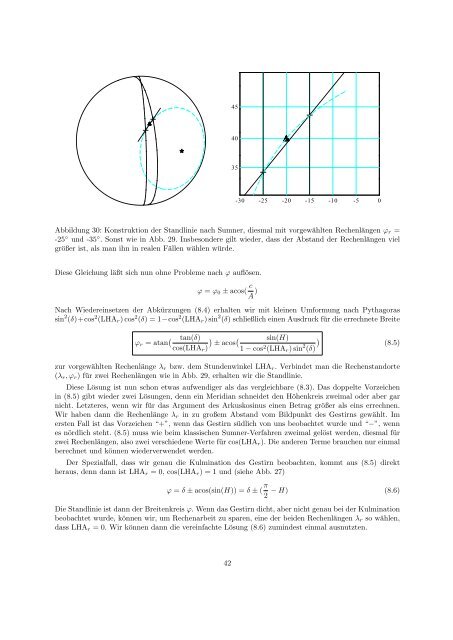
Abbildung 30: Konstruktion der Standlinie nach Sumner, diesmal mit vorgewählten Rechenlängen ϕr =
-25 ◦ und -35 ◦ . Sonst wie in Abb. 29. Insbesondere gilt wieder, dass der Abstand der Rechenlängen viel
größer ist, als man ihn in realen Fällen wählen würde.
Diese Gleichung läßt sich nun ohne Probleme nach ϕ auflösen.
ϕ = ϕ0 ± acos( c
A )
Nach Wiedereinsetzen der Abkürzungen (8.4) erhalten wir mit kleinen Umformung nach Pythagoras
sin 2 (δ)+cos 2 (LHAr) cos 2 (δ) = 1−cos 2 (LHAr) sin 2 (δ) schließlich einen Ausdruck für die errechnete Breite
ϕr = atan � tan(δ) � � sin(H)
± acos
cos(LHAr) 1 − cos2 (LHAr) sin 2 �
(δ)
zur vorgewählten Rechenlänge λr bzw. dem Stundenwinkel LHAr. Verbindet man die Rechenstandorte
(λr, ϕr) für zwei Rechenlängen wie in Abb. 29, erhalten wir die Standlinie.
Diese Lösung ist nun schon etwas aufwendiger als das vergleichbare (8.3). Das doppelte Vorzeichen
in (8.5) gibt wieder zwei Lösungen, denn ein Meridian schneidet den Höhenkreis zweimal oder aber gar
nicht. Letzteres, wenn wir für das Argument des Arkuskosinus einen Betrag größer als eins errechnen.
Wir haben dann die Rechenlänge λr in zu großem Abstand vom Bildpunkt des Gestirns gewählt. Im
ersten Fall ist das Vorzeichen “+”, wenn das Gestirn südlich von uns beobachtet wurde und “−”, wenn
es nördlich steht. (8.5) muss wie beim klassischen Sumner-Verfahren zweimal gelöst werden, diesmal für
zwei Rechenlängen, also zwei verschiedene Werte für cos(LHAr). Die anderen Terme brauchen nur einmal
berechnet und können wiederverwendet werden.
Der Spezialfall, dass wir genau die Kulmination des Gestirn beobachten, kommt aus (8.5) direkt
heraus, denn dann ist LHAr = 0, cos(LHAr) = 1 und (siehe Abb. 27)
(8.5)
ϕ = δ ± acos(sin(H)) = δ ± ( π
− H) (8.6)
2
Die Standlinie ist dann der Breitenkreis ϕ. Wenn das Gestirn dicht, aber nicht genau bei der Kulmination
beobachtet wurde, können wir, um Rechenarbeit zu sparen, eine der beiden Rechenlängen λr so wählen,
dass LHAr = 0. Wir können dann die vereinfachte Lösung (8.6) zumindest einmal ausnutzten.
42